सादिशों का संकलन: Difference between revisions

Listen

Latest revision as of 17:12, 11 January 2024

Addition of vectors

सदिशों का संकलन गणित और भौतिकी में एक मौलिक अवधारणा है। इसमें उनके परिणामी सदिश को ढूँढने के लिए दो या दो से अधिक सदिशों को संकलित करना निहित है।

माप व संकलन

सदिश का माप उसके परिमाण (लंबाई) और दिशा दोनों पर निर्भर करता है। वे तीरों द्वारा दर्शाए जाते हैं, जहां तीर की लंबाई सदिश के परिमाण से मेल खाती है, और तीर की दिशा,सदिश की दिशा का प्रतिनिधित्व करती है।

संकलन प्रक्रिया

सादिशों (वैक्टरों) के ज्यामितीय शीर्ष से पार्श्व (हेड-टू-टेल) जोड़ का चित्रण

दो सदिशों का संकलित के लिए, उन्हें शीर्ष (सिर) से पार्श्व (पूंछ) तक रखना होगा। दो सादिशों,सदिश $A$ और सदिश $B$ को संकलित करने की चरण दर चरण प्रक्रीया , पर विचार करें।

सदिश $A$ को एक तीर के रूप में बनाकर प्रारंभ करें, जो इसके परिमाण और दिशा को दर्शाता है।उदाहरण के लिए, यदि सदिश $A$ का परिमाण $4$ इकाई है और यह दाईं ओर निर्देशित है, तो दाईं ओर इंगित करते हुए $4$ इकाई की लंबाई वाला एक तीर खींचें।
इसके बाद, सदिश $A$ के शीर्ष से आरंभ होने वाले सदिश $B$ को इस तरह बनाएं कि सदिश $B$ का पार्श्व सदिश $A$ के शीर्ष के साथ मेल खाए। सदिश $B$ की परिमाण और दिशा को सटीक रूप से प्रदर्शित किया जाना चाहिए। मान लीजिए कि सदिश $B$ का परिमाण $3$ इकाई है और यह ऊपर की ओर निर्देशित है। सदिश $A$ के शीर्ष से ऊपर की ओर इंगित करते हुए $3$ इकाइयों की लंबाई वाला एक तीर बनाएं।
अब, सदिश $A$ के शीर्षे से सदिश $B$ के शीर्षे तक एक सीधी रेखा खींचिए। यह रेखा परिणामी सदिश को दर्शाती है, जो सदिश $A$ और सदिश $B$ का योग है परिणामी सदिश, वह सदिश है, जो सदिश $A$ की पार्श्व से शुरू होता है और सदिश $B$ के शीर्ष पर समाप्त होता है। इस रेखा की लंबाई और दिशा को मापकर इसका परिमाण और दिशा निर्धारित की जा सकती है।
अंत में, परिणामी सदिश $R$ को सदिश $A$ और सदिश $B$ के योग के रूप में चिन्हित (लेबल) करें, जो इसके (परिणामी सदिश $R$ ) के परिमाण और दिशा को दर्शाता है।

परिणामी सदिश

परिणामी सदिश के परिमाण और दिशा की ठीक-ठीक गणना करने के लिए पाइथागोरस प्रमेय और त्रिकोणमिति का उपयोग करा जा सकता है।

परिणामी सदिश का परिमाण सूत्र का उपयोग करके पाया जा सकता है: $R={\sqrt {(A)^{2}+(B)^{2}}}$ का परिमाण।
परिणामी सदिश की दिशा, परिणामी सदिश और एक संदर्भ दिशा, जैसे कि धनात्मक $x-$ अक्ष के बीच के कोण की स्पर्शरेखा का उपयोग करके पाया जा सकती है ।

संक्षेप में

दो सादिशों को सफलतापूर्वक जोड़ते समय और उनका परिणामी सदिश पाने में समय परिमाण और दिशा दोनों पर ध्यान रखें, क्योंकि वे दोनों परिणामी सदिश को निर्धारित करने में महत्वपूर्ण भूमिका निभाते हैं।

@@ Line 1: / Line 1: @@
 Addition of vectors
-सदिशों का संकलन गणित और भौतिकी में एक मौलिक अवधारणा है। इसमें उनके परिणामी सदिश को खोजने के लिए दो या दो से अधिक सदिशों को संकलित करना शामिल है।
+सदिशों का संकलन गणित और भौतिकी में एक मौलिक अवधारणा है। इसमें उनके परिणामी सदिश को ढूँढने  के लिए दो या दो से अधिक सदिशों को संकलित करना निहित  है।
 == माप  व संकलन ==
-सदिश का माप उसके परिमाण (लंबाई) और दिशा दोनों पर निर्भर करता है। वे तीरों द्वारा दर्शाए जाते हैं, जहां तीर की लंबाई सदिश के परिमाण से मेल खाती है, और तीर की दिशा सदिश की दिशा का प्रतिनिधित्व करती है।
+सदिश का माप उसके परिमाण (लंबाई) और दिशा दोनों पर निर्भर करता है। वे तीरों द्वारा दर्शाए जाते हैं, जहां तीर की लंबाई सदिश के परिमाण से मेल खाती है, और तीर की दिशा,सदिश की दिशा का प्रतिनिधित्व करती है।
 == संकलन प्रक्रिया ==
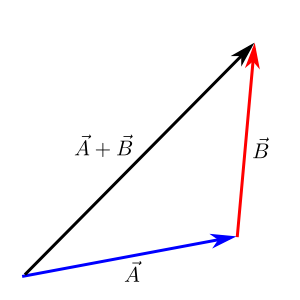
-दो सदिशों का संकलित के लिए, आपको उन्हें शीर्ष (सिर) से पार्श्व (पूंछ) तक रखना होगा। दो सादिशों,सदिश <math>A</math> और सदिश <math>B</math> को संकलित करने की चरण दर चरण  प्रक्रीया ,  पर विचार करें।
+[[File:Head-to-tail Addition.png|thumb|सादिशों (वैक्टरों) के ज्यामितीय शीर्ष से पार्श्व (हेड-टू-टेल) जोड़ का चित्रण]]
+दो सदिशों का संकलित के लिए,  उन्हें शीर्ष (सिर) से पार्श्व (पूंछ) तक रखना होगा। दो सादिशों,सदिश <math>A</math> और सदिश <math>B</math> को संकलित करने की चरण दर चरण  प्रक्रीया ,  पर विचार करें।
 # सदिश <math>A</math> को एक तीर के रूप में बनाकर प्रारंभ करें, जो इसके परिमाण और दिशा को दर्शाता है।उदाहरण के लिए, यदि सदिश <math>A</math> का परिमाण <math>4</math> इकाई है    और यह दाईं ओर निर्देशित है, तो दाईं ओर इंगित करते हुए <math>4</math> इकाई की लंबाई वाला एक तीर खींचें।
-# इसके बाद, सदिश <math>A</math> के शीर्ष से आरंभ होने वाले सदिश <math>B</math> को इस तरह बनाएं कि सदिश <math>B</math> का पार्श्व सदिश <math>A</math> के शीर्ष के साथ मेल खाए। सदिश <math>B</math> की परिमाण और दिशा को सटीक रूप से प्रदर्शित किया जाना चाहिए। मान लीजिए कि सदिश <math>B</math> का परिमाण 3 इकाई है और यह ऊपर की ओर निर्देशित है। सदिश <math>A</math> के शीर्ष से ऊपर की ओर इशारा करते हुए 3 इकाइयों की लंबाई वाला एक तीर बनाएं।
+# इसके बाद, सदिश <math>A</math> के शीर्ष से आरंभ होने वाले सदिश <math>B</math> को इस तरह बनाएं कि सदिश <math>B</math> का पार्श्व सदिश <math>A</math> के शीर्ष के साथ मेल खाए। सदिश <math>B</math> की परिमाण और दिशा को सटीक रूप से प्रदर्शित किया जाना चाहिए। मान लीजिए कि सदिश <math>B</math> का परिमाण <math>3 </math> इकाई है और यह ऊपर की ओर निर्देशित है। सदिश <math>A</math> के शीर्ष से ऊपर की ओर इंगित करते हुए <math>3 </math> इकाइयों की लंबाई वाला एक तीर बनाएं।
-# अब, सदिश <math>A</math> के शीर्षे से सदिश <math>B</math> के शीर्षे तक एक सीधी रेखा खींचिए। यह रेखा परिणामी सदिश को दर्शाती है, जो सदिश <math>A</math> और सदिश <math>B</math> का योग है    परिणामी सदिश, वह सदिश है, जो सदिश <math>A</math> की पार्श्व से शुरू होता है और सदिश <math>B</math> के शीर्ष पर समाप्त होता है। इस रेखा की लंबाई और दिशा को मापकर इसका परिमाण और दिशा निर्धारित की जा सकती है।
+# अब, सदिश <math>A</math> के शीर्षे से सदिश <math>B</math> के शीर्षे तक एक सीधी रेखा खींचिए। यह रेखा परिणामी सदिश को दर्शाती है, जो सदिश <math>A</math> और सदिश <math>B</math> का योग है परिणामी सदिश, वह सदिश है, जो सदिश <math>A</math> की पार्श्व से शुरू होता है और सदिश <math>B</math> के शीर्ष पर समाप्त होता है। इस रेखा की लंबाई और दिशा को मापकर इसका परिमाण और दिशा निर्धारित की जा सकती है।
-# अंत में, परिणामी सदिश <math>R</math> को सदिश <math>A</math> और सदिश <math>B</math> के योग के रूप में चिन्हित (लेबल) करें, जो इसके (परिणामी सदिश <math>R</math>) के परिमाण और दिशा को दर्शाता है। परिणामी सदिश के परिमाण और दिशा की ठीक-ठीक गणना करने के लिए पाइथागोरस प्रमेय और त्रिकोणमिति का उपयोग करा जा सकता है।
+# अंत में, परिणामी सदिश <math>R</math> को सदिश <math>A</math> और सदिश <math>B</math> के योग के रूप में चिन्हित (लेबल) करें, जो इसके (परिणामी सदिश <math>R</math>) के परिमाण और दिशा को दर्शाता है।
+== परिणामी सदिश ==
+परिणामी सदिश के परिमाण और दिशा की ठीक-ठीक गणना करने के लिए पाइथागोरस प्रमेय और त्रिकोणमिति का उपयोग करा जा सकता है।
 *    परिणामी सदिश का परिमाण सूत्र का उपयोग करके पाया जा सकता है: <math>R=\sqrt {(A)^2+(B)^2}</math> का परिमाण।
-*    परिणामी सदिश की दिशा, परिणामी सदिश और एक संदर्भ दिशा, जैसे कि धनात्मक <math>x-</math>अक्ष के बीच के कोण की स्पर्शरेखा का उपयोग करके पाया जा सकती है
+*    परिणामी सदिश की दिशा, परिणामी सदिश और एक संदर्भ दिशा, जैसे कि धनात्मक <math>x-</math>अक्ष के बीच के कोण की स्पर्शरेखा का उपयोग करके पाया जा सकती है ।
+== संक्षेप में ==
 दो सादिशों को सफलतापूर्वक जोड़ते समय और उनका परिणामी सदिश पाने में समय परिमाण और दिशा दोनों पर ध्यान रखें, क्योंकि वे दोनों परिणामी सदिश को निर्धारित करने में महत्वपूर्ण भूमिका निभाते हैं।
-[[Category:समतल में गति]]
+[[Category:समतल में गति]][[Category:भौतिक विज्ञान]][[Category:कक्षा-11]]