सर्वनिष्ट(समुच्चय): Difference between revisions
(images added) |
No edit summary |
||
| Line 51: | Line 51: | ||
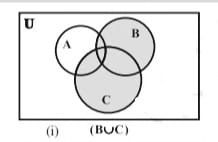
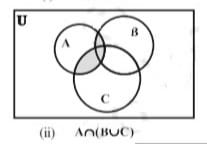
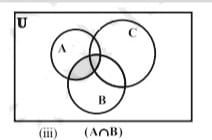
नीचे दिए गए वेन आरेखों [चित्र (I) - (V)] द्वारा इस बात को सरलता से देख सकते हैं। | नीचे दिए गए वेन आरेखों [चित्र (I) - (V)] द्वारा इस बात को सरलता से देख सकते हैं। | ||
[[File:I.jpg|thumb|चित्र-1-समुच्चयों का सर्वनिष्ठ I]] | [[File:I.jpg|thumb|चित्र-1-समुच्चयों का सर्वनिष्ठ I|left]] | ||
[[File:II.jpg|thumb|चित्र-2-समुच्चयों का सर्वनिष्ठ II]] | [[File:II.jpg|thumb|चित्र-2-समुच्चयों का सर्वनिष्ठ II]] | ||
[[File:III.jpg|thumb|चित्र-3-समुच्चयों का सर्वनिष्ठ III]] | [[File:III.jpg|thumb|चित्र-3-समुच्चयों का सर्वनिष्ठ III|left]] | ||
[[File:IV.jpg|thumb|चित्र-4-समुच्चयों का सर्वनिष्ठ IV]] | [[File:IV.jpg|thumb|चित्र-4-समुच्चयों का सर्वनिष्ठ IV]] | ||
[[File:V.jpg|thumb|चित्र-समुच्चयों का सर्वनिष्ठ V]] | [[File:V.jpg|thumb|चित्र-समुच्चयों का सर्वनिष्ठ V|center]] | ||
[[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | ||
Revision as of 22:39, 6 November 2024
समुच्चयों का सर्वनिष्ठ
समुच्चय और का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो और दोनों में उभयनिष्ठ है। प्रतीक '' का प्रयोग सर्वनिष्ठ को निरूपित करने के लिए किया जाता है। समुच्चय और का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो और दोनों में हों। प्रतीकात्मक रूप में हम लिखते हैं कि और
उदाहरण
मान लीजिए किऔर । ज्ञात कीजिए।
हम देखते हैं कि
उदाहरण 1: उपर्युक्त उदाहरण के समुच्चय और पर विचार करते हुए | ज्ञात कीजिए।
हल: हम देखते हैं कि केवल और ही ऐसे अवयव हैं जो और दोनों में उभयनिष्ठ हैं। अतः
उदाहरण 2: मान लीजिए कि और ज्ञात कीजिए और इस प्रकार दिखाइए कि ।
हल: हल हम देखते हैं कि हम ध्यान देते हैं कि और
परिभाषा
समुच्चय और का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो और दोनों में हो। प्रतीकात्मक रूप में, हम लिखते हैं कि और
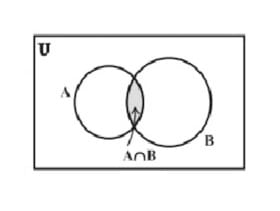
चित्र में छायांकित भाग, और के सर्वनिष्ठ को प्रदर्शित करता है।
यदि और ऐसे दो समुच्चय हों कि, तो और असंयुक्त समुच्चय कहलाते हैं। उदाहरण के लिए मान लीजिए कि और , तो और असंयुक्त समुच्चय हैं, क्योंकि और में कोई भी अवयव उभयनिष्ठ नहीं है। असंयुक्त समुच्चयों को वेन आरेख द्वारा निरूपित किया जा सकता है, जैसा चित्र में प्रदर्शित है। उपर्युक्त आरेख में और असंयुक्त समुच्चय हैं।
सर्वनिष्ठ संक्रिय के कुछ गुणधर्म
(i) ( क्रम विनिमय नियम )
(ii) (साहचर्य नियम)
(iii) ( और के नियम)
(iv) ( वर्गसम नियम )
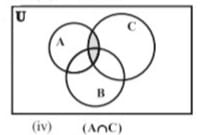
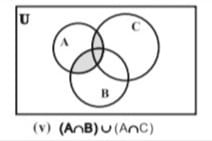
(v) ( वितरण या बंटन नियम)
अर्थात् वितरित होता है पर
नीचे दिए गए वेन आरेखों [चित्र (I) - (V)] द्वारा इस बात को सरलता से देख सकते हैं।