समुच्चयों का अंतर: Difference between revisions
(added content) |
(images added) |
||
| Line 12: | Line 12: | ||
'''उदाहरण 2:''' मान लीजिए कि <math>V = \{a,e,i,o,u\}</math> तो <math>B = \{a, i, k, u\}</math>, तो <math>V-B</math> और <math>B-V</math> ज्ञात कीजिए। | '''उदाहरण 2:''' मान लीजिए कि <math>V = \{a,e,i,o,u\}</math> तो <math>B = \{a, i, k, u\}</math>, तो <math>V-B</math> और <math>B-V</math> ज्ञात कीजिए। | ||
हल यहाँ, V - B = { | '''हल''' यहाँ, <math>V-B=\{e,o\}</math> , क्योंकि अवयव <math>e,o</math> समुच्चय <math>V</math> में हैं किंतु <math>B</math> में नहीं है तथा - <math>B-V=\{k\}</math>, क्योंकि अवयव <math>k</math> समुच्चय <math>B</math> में है परंतु <math>V</math> में नहीं है। | ||
[[File:समुच्चयों का अंतर-1.jpg|thumb|चित्र-1 समुच्चयों का अंतर ]] | |||
हम यह अवश्य ध्यान देते हैं कि <math>V-B\neq B-V</math> समुच्चय निर्माण संकेतन का प्रयोग करते हुए हम समुच्चयों के अंतर की परिभाषा को पुनः इस प्रकार लिख सकते हैं: | |||
<math>A-B=\{x:x\in A </math> और <math>x\not\in B\}</math> | |||
A - | दो समुच्चयों <math>A</math> और <math>B</math> के अंतर को वेन आरेख द्वारा दर्शाया जा सकता है जैसा कि चित्र-1 में प्रदर्शित है। छायांकित भाग दो समुच्चय <math>A</math> और <math>B</math> के अंतर को दर्शाता है। | ||
== टिप्पणी == | |||
[[File:समुच्चयों का अंतर-2.jpg|thumb|चित्र-2 समुच्चयों का अंतर]] | |||
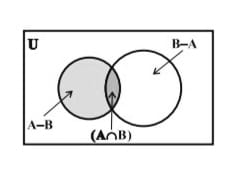
समुच्चय <math>A-B, A\cap B</math> और <math>B-A</math> परस्पर असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि चित्र-2 में प्रदर्शित है। | |||
असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि | |||
Revision as of 12:34, 7 November 2024
समुच्चयों का अंतर
समुच्चयों और का अंतर उन अवयवों का समुच्चय है जो में हैं किंतु में नहीं हैं, जब कि और को इसी क्रम में लिया जाए। प्रतीतात्मक रूप में इसे लिखते हैं और “ अंतर ” पढ़ते हैं।
उदाहरण 1: मान लेते हैं कि , और ज्ञात कीजिए ।
हल हम प्राप्त करते हैं कि,, क्योंकि अवयव समुच्चय में हैं किंतु में नहीं हैं तथा , क्योंकि अवयव , में है किंतु में नहीं है। हम देखते हैं कि
उदाहरण 2: मान लीजिए कि तो , तो और ज्ञात कीजिए।
हल यहाँ, , क्योंकि अवयव समुच्चय में हैं किंतु में नहीं है तथा - , क्योंकि अवयव समुच्चय में है परंतु में नहीं है।
हम यह अवश्य ध्यान देते हैं कि समुच्चय निर्माण संकेतन का प्रयोग करते हुए हम समुच्चयों के अंतर की परिभाषा को पुनः इस प्रकार लिख सकते हैं:
और
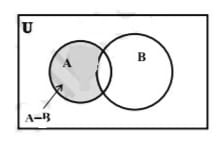
दो समुच्चयों और के अंतर को वेन आरेख द्वारा दर्शाया जा सकता है जैसा कि चित्र-1 में प्रदर्शित है। छायांकित भाग दो समुच्चय और के अंतर को दर्शाता है।
टिप्पणी
समुच्चय और परस्पर असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि चित्र-2 में प्रदर्शित है।