गणना का आधारभूत सिद्धांत: Difference between revisions

Latest revision as of 21:18, 11 November 2024

गणना का आधारभूत सिद्धांत एक गणितीय नियम है जो दो या दो से अधिक घटनाओं के होने पर किसी स्थिति में संभावित परिणामों की कुल संख्या की गणना करता है:

गणना का आधारभूत सिद्धांत

गणना सिद्धांत एक नियम है जिसका उपयोग किसी स्थिति में संभावित परिणामों की कुल संख्या को गिनने के लिए किया जाता है। यह बताता है कि यदि किसी काम को करने के $n$ तरीके हैं, और उसके बाद किसी दूसरी चीज़ को करने के $m$ तरीके हैं, तो इन दोनों क्रियाओं को करने के $n\times m$ तरीके हैं। दूसरे शब्दों में, $n$ के लिए एक विकल्प और $m$ के लिए एक विकल्प चुनते समय, दोनों क्रियाओं को करने के $n\times m$ अलग-अलग उपाय या विधि हैं।

आईए हम निम्नलिखित समस्या पर विचार करें:

चित्र-1 गणना का आधारभूत सिद्धांत 1

उदाहरण 1 :

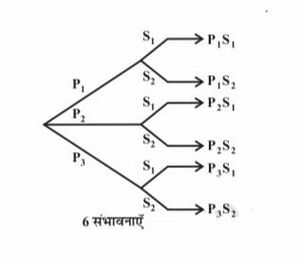
माधव के पास $P_{1},P_{2},P_{3}$ तीन पैंट तथा $S_{1},S_{2}$ दो कमीज़ें हैं। उसके पास पहनने के लिए पैंट तथा कमीज़ के कितने भिन्न भिन्न जोड़े(युग्म) हैं ? एक पैंट चुनने के लिए $3$ तरीके हैं, क्योंकि चयन के लिए $3$ पैंट उपलब्ध हैं। इसी प्रकार एक कमीज़ का चयन $2$ तरह से किया जा सकता है। पैंट के प्रत्येक चयन के लिए कमीज़ के चयन के $2$ विकल्प संभव हैं। अतः पैंट तथा कमीज़ के जोड़ों के चयन की संख्या $3\times 2=6$ है। इस तथ्य को चित्र-1 में स्पष्ट किया गया है।

आइए हम इसी प्रकार की एक दूसरी समस्या पर विचार करें:

चित्र-2 गणना का आधारभूत सिद्धांत 2

उदाहरण 2 :

माया के पास $2$ बस्ते $3$ खाने के डिब्बे तथा $2$ पानी की बोतलें हैं। वह इन वस्तुओं को किस प्रकार से ले जा सकती है ( प्रत्येक में से एक चुन कर ) ।

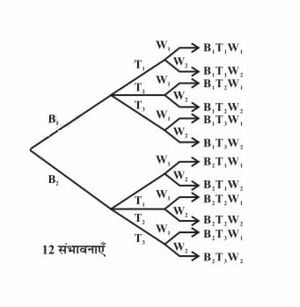
एक बस्ते को $2$ भिन्न तरीकों से चुना जा सकता है। एक बस्ते के चुने जाने के बाद, एक खाने के डिब्बे को चुनने के $3$ भिन्न तरीके हैं। इस प्रकार बस्ते और खाने के डिब्बे के जोड़ों की संख्या $2\times 3=6$ है। इनमें से प्रत्येक जोड़े के लिए एक पानी की बोतल को चुनने के $2$ भिन्न तरीके हैं। अतः शबनम द्वारा इन वस्तुओं को स्कूल ले जाने के कुल $6\times 2=12$ भिन्न तरीके हैं। यदि हम दो बस्तों को $B_{1},B_{2}$ तीन खाने के डिब्बों को $T_{1},T_{2},T_{3}$ तथा दो पानी की बोतलों को $W_{1},W_{2}$ , नाम दें, तो इन संभावनाओं को नीचे बनी आकृति द्वारा स्पष्ट किया जा सकता है (चित्र-2) ।

वस्तुत: उपर्युक्त प्रकार की समस्याओं को निम्नलिखित सिद्धांत के प्रयोग द्वारा सरल किया जाता है, जिसे गणना का आधारभूत सिद्धांत अथवा केवल गणन सिद्धांत कहते हैं और जिसका कथन इस प्रकार है,

"यदि एक घटना $m$ भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना $n$ भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या $m\times n$ है।"

ऊपर वर्णित सिद्धांत का घटनाओं की सीमित संख्या के लिए व्यापकीकरण किया जा सकता है। उदाहरणार्थ, $3$ घटनाओं के लिए, यह सिद्धांत निम्नलिखित प्रकार से होगा:

'यदि एक घटना $m$ भिन्न तरीकों से घटित हो सकती है, इसके उपरांत एक दूसरी घटना $n$ भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक तीसरी घटना $p$ भिन्न तरीकों से घटित हो सकती है, तो तीनों घटनाओं के घटित होने के भिन्न तरीकों की कुल संख्या, दिए हुए क्रम में, $m\times n\times p$ है।"

प्रथम प्रश्न में, पैंट तथा कमीज के जोड़ों को पहनने की अभीष्ट संख्या, निम्नलिखित घटनाओं के उत्तरोत्तर घटित होने के विभिन्न विन्यासों की संख्या के तुल्य है:

(i) एक पैंट के चयन की घटना

(ii) एक कमीज़ के चयन की घटना

दूसरे प्रश्न में विन्यासों की अभीष्ट संख्या, निम्नलिखित घटनाओं के उत्तरोत्तर घटित होने के विभिन्न विन्यासों की संख्या के समान है:

(i) एक बस्ते के चयन की घटना,

(ii) एक खाने के डिब्बे के चयन की घटना,

(iii) एक पानी की बोतल के चयन की घटना।

यहाँ दोनों में से प्रत्येक प्रश्न में घटनाएँ अनेक संभव क्रमों में घटित हो सकती हैं परंतु हम इन संभव क्रमों में से किसी एक का चयन करते हैं और इस चयनित क्रम में घटनाओं के घटित होने के विभिन्न विन्यासों की गणना करते हैं।

@@ Line 2: / Line 2: @@
 == गणना का आधारभूत सिद्धांत  ==
-गणना सिद्धांत एक नियम है जिसका उपयोग किसी स्थिति में संभावित परिणामों की कुल संख्या को गिनने के लिए किया जाता है। यह बताता है कि यदि किसी काम को करने के <math>n</math> तरीके हैं, और उसके बाद किसी दूसरी चीज़ को करने के <math>m</math> तरीके हैं, तो इन दोनों क्रियाओं को करने के <math>n \times m</math> तरीके हैं। दूसरे शब्दों में, <math>n</math> के लिए एक विकल्प और <math>m</math> के लिए एक विकल्प चुनते समय, दोनों क्रियाओं को करने के <math>n \times m</math> अलग-अलग उपाय या विधि हैं।
+गणना सिद्धांत एक नियम है जिसका उपयोग किसी स्थिति में संभावित परिणामों की कुल [[संख्या]] को गिनने के लिए किया जाता है। यह बताता है कि यदि किसी काम को करने के <math>n</math> तरीके हैं, और उसके बाद किसी दूसरी चीज़ को करने के <math>m</math> तरीके हैं, तो इन दोनों क्रियाओं को करने के <math>n \times m</math> तरीके हैं। दूसरे शब्दों में, <math>n</math> के लिए एक विकल्प और <math>m</math> के लिए एक विकल्प चुनते समय, दोनों क्रियाओं को करने के <math>n \times m</math> अलग-अलग उपाय या विधि हैं।
 आईए हम निम्नलिखित समस्या पर विचार करें:
@@ Line 20: / Line 20: @@
 वस्तुत: उपर्युक्त प्रकार की समस्याओं को निम्नलिखित सिद्धांत के प्रयोग द्वारा सरल किया जाता है, जिसे '''गणना का आधारभूत सिद्धांत''' अथवा केवल '''गणन सिद्धांत''' कहते हैं और जिसका कथन इस प्रकार है,
-"यदि एक घटना <math>m</math> भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना <math>n</math> भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या <math>m\times n</math> है।"
+"यदि एक [[घटना(प्रायिकता)|घटना]] <math>m</math> भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना <math>n</math> भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या <math>m\times n</math> है।"
 ऊपर वर्णित सिद्धांत का घटनाओं की सीमित संख्या के लिए व्यापकीकरण किया जा सकता है। उदाहरणार्थ, <math>3</math> घटनाओं के लिए, यह सिद्धांत निम्नलिखित प्रकार से होगा: