धन पूर्णांकों के लिए द्विपद प्रमेय: Difference between revisions
No edit summary |
No edit summary |
||
| Line 31: | Line 31: | ||
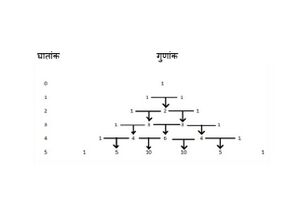
[[File:धन पूर्णांकों के लिए द्विपद प्रमेय.jpg|thumb|चित्र-1 धन पूर्णांकों के लिए द्विपद प्रमेय]] | [[File:धन पूर्णांकों के लिए द्विपद प्रमेय.jpg|thumb|चित्र-1 धन पूर्णांकों के लिए द्विपद प्रमेय]] | ||
क्या हम इस सारणी में अगली पंक्ति लिखने के लिए किसी प्रतिरूप का अवलोकन करते हैं? हाँ। यह देखा जा सकता है कि घात <math>1</math> की पंक्ति में लिखे <math>1</math> और <math>1</math> का योग घात <math>2</math> की पंक्ति के लिए <math>2</math> देता है । घात <math>2</math> की पंक्ति में लिखे <math>1</math> और <math>2</math> तथा <math>2</math> और <math>1</math> का योग घात <math>3</math> की पंक्ति के लिए <math>3</math> और <math>3</math> देता है और आगे भी इसी प्रकार <math>1</math> पुनः प्रत्येक पंक्ति के प्रारंभ व अंत में स्थित है। इस प्रक्रिया को किसी भी इच्छित घात तक के लिए लिखा जा सकता है। | |||
क्या हम इस सारणी में अगली पंक्ति लिखने के लिए किसी प्रतिरूप का अवलोकन करते हैं? हाँ। यह देखा जा सकता है कि घात <math>1</math> की पंक्ति में लिखे <math>1</math> और <math>1</math> का योग घात <math>2</math> की पंक्ति के लिए <math>2</math> देता है । घात <math>2</math> की पंक्ति में लिखे <math>1</math> और <math>2</math> तथा <math>2</math> और <math>1</math> का योग घात <math>3</math> की पंक्ति के लिए <math>3</math> और <math>3</math> देता है और आगे भी इसी प्रकार <math>1</math> पुनः प्रत्येक पंक्ति के प्रारंभ व अंत में स्थित है। इस प्रक्रिया को किसी भी इच्छित घात तक के लिए लिखा जा सकता है। | |||
[[File:धनात्मक समाकलन गुणांक.jpg|thumb|चित्र-2 धनात्मक समाकलन गुणांक]] | [[File:धनात्मक समाकलन गुणांक.jpg|thumb|चित्र-2 धनात्मक समाकलन गुणांक]] | ||
| Line 54: | Line 42: | ||
(चित्र-2) धनात्मक समाकलन गुणांकों के लिए द्विपद प्रमेय का संक्षिप्त परिचय है। | |||
== गुणधर्म == | == गुणधर्म == | ||
Revision as of 19:23, 16 November 2024
धनात्मक समाकलन पूर्णांकों के लिए द्विपद प्रमेय बताता है कि किसी विस्तार में पदों की कुल संख्या प्रायः विस्तार के पूर्णांक से एक अधिक होती है।
उदाहरण के लिए, के विस्तार में, पदों की संख्या है, जहाँ कोई भी धनात्मक पूर्णांक है।
द्विपद प्रमेय यह भी बताता है कि के रूप के पद को के रूप में कैसे विस्तारित और व्यक्त किया जाए, जहां घातांक और गैर-ऋणात्मक पूर्णांक हैं जो शर्त को संतुष्ट करते हैं।
द्विपद प्रमेय का उपयोग को विस्तारित करने के लिए किया जा सकता है, जहाँ कोई भी परिमेय संख्या है।
धन पूर्णांकों के लिए द्विपद प्रमेय
आइए पूर्व में की गई निम्नलिखित सर्वसमिकाओं पर हम विचार करें:
इन प्रसारों में हम देखते हैं कि
(i) प्रसार में पदों की कुल संख्या, घातांक से अधिक है। उदाहरणत: के प्रसार में का घात है जबकि प्रसार में कुल पदों की संख्या है।
(ii) प्रसार के उत्तरोत्तर पदों में प्रथम की घातें एक के क्रम से घट रही हैं जबकि द्वितीय राशि की घातें एक के क्रम से बढ़ रही हैं।
(iii) प्रसार के प्रत्येक पद में तथा की घातों का योग समान है और की घात के बराबर है।
अब हम के उपरोक्त विस्तारों में विभिन्न पदों के गुणांकों को निम्न प्रकार व्यवस्थित करते हैं (चित्र- 1)
क्या हम इस सारणी में अगली पंक्ति लिखने के लिए किसी प्रतिरूप का अवलोकन करते हैं? हाँ। यह देखा जा सकता है कि घात की पंक्ति में लिखे और का योग घात की पंक्ति के लिए देता है । घात की पंक्ति में लिखे और तथा और का योग घात की पंक्ति के लिए और देता है और आगे भी इसी प्रकार पुनः प्रत्येक पंक्ति के प्रारंभ व अंत में स्थित है। इस प्रक्रिया को किसी भी इच्छित घात तक के लिए लिखा जा सकता है।
(चित्र-2) धनात्मक समाकलन गुणांकों के लिए द्विपद प्रमेय का संक्षिप्त परिचय है।
गुणधर्म
द्विपद प्रमेय के कुछ गुण यहां दिए गए हैं:
- पद से पद तक, के घातांक से घटते हैं, जबकि के घातांक से बढ़ते हैं।
- , जहाँ एक गैर-ऋणात्मक पूर्णांक है और
- और का मान के बराबर है।