दीर्घवृत्त: Difference between revisions
(added content) |
(image added) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
दीर्घवृत्त शंकु परिच्छेद का एक अभिन्न अंग है और गुणों में वृत्त के समान है। वृत्त के विपरीत, दीर्घवृत्त आकार में अंडाकार होता है। दीर्घवृत्त की उत्केन्द्रता एक से कम होती है, और यह बिंदुओं के बिन्दुपथ को दर्शाता है, जिनकी दो नाभियों से दूरियों का योग एक स्थिर मान होता है। हमारे दैनिक जीवन में दीर्घवृत्त के सरल उदाहरण दो-आयामी रूप में अंडे का आकार, खेल स्टेडियम में दौड़ना आदि हैं। | दीर्घवृत्त [[शंकु के परिच्छेद|शंकु परिच्छेद]] का एक अभिन्न अंग है और गुणों में [[वृत्त]] के समान है। वृत्त के विपरीत, दीर्घवृत्त आकार में अंडाकार होता है। दीर्घवृत्त की उत्केन्द्रता एक से कम होती है, और यह बिंदुओं के बिन्दुपथ को दर्शाता है, जिनकी दो नाभियों से दूरियों का योग एक स्थिर मान होता है। हमारे दैनिक जीवन में दीर्घवृत्त के सरल उदाहरण दो-आयामी रूप में अंडे का आकार, खेल स्टेडियम में दौड़ना आदि हैं। | ||
यहाँ हम दीर्घवृत्त की परिभाषा, दीर्घवृत्त के समीकरण की व्युत्पत्ति और दीर्घवृत्त के समीकरणों के विभिन्न मानक रूपों को जानने का लक्ष्य रखेंगे। | यहाँ हम दीर्घवृत्त की परिभाषा, दीर्घवृत्त के समीकरण की व्युत्पत्ति और दीर्घवृत्त के समीकरणों के विभिन्न मानक रूपों को जानने का लक्ष्य रखेंगे। | ||
== परिचय == | == परिचय == | ||
गणित में, दीर्घवृत्त एक | गणित में, दीर्घवृत्त एक संवृत वक्र होता है जो दो लंबवत अक्षों के संबंध में सममित होता है। इसे एक समतल में सभी बिंदुओं के समूह के रूप में परिभाषित किया जा सकता है, जैसे कि वक्र पर किसी भी बिंदु से दो निश्चित बिंदुओं (जिन्हें नाभि(फोकस)कहा जाता है) तक की दूरी का योग स्थिर होता है। निश्चित बिंदुओं को नाभि कहा जाता है और उन्हें <math>F</math> और <math>F'</math> द्वारा दर्शाया जाता है। | ||
दीर्घवृत्त शंकु वर्गों में से एक है, जो शंकु का उस समतल से प्रतिच्छेदन है जो शंकु के आधार को प्रतिच्छेद नहीं करता है। | दीर्घवृत्त शंकु वर्गों में से एक है, जो शंकु का उस समतल से प्रतिच्छेदन है जो शंकु के आधार को प्रतिच्छेद नहीं करता है। | ||
| Line 14: | Line 14: | ||
दीर्घवृत्त के सामान्य समीकरण का उपयोग निर्देशांक तल में दीर्घवृत्त को बीजगणितीय रूप से दर्शाने के लिए किया जाता है। दीर्घवृत्त का समीकरण इस प्रकार दिया जा सकता है, | दीर्घवृत्त के सामान्य समीकरण का उपयोग निर्देशांक तल में दीर्घवृत्त को बीजगणितीय रूप से दर्शाने के लिए किया जाता है। दीर्घवृत्त का समीकरण इस प्रकार दिया जा सकता है, | ||
<math>\frac{x^2}{ a^2}+\frac{y^2 }{ b^2}=1</math> | |||
, जहाँ | , जहाँ | ||
* 'a' अर्ध- | * '<math>a</math>' अर्ध-दीर्घ अक्ष (दीर्घ अक्ष की लंबाई का आधा) को दर्शाता है | ||
* 'b' अर्ध-लघु अक्ष (लघु अक्ष की लंबाई का आधा) को दर्शाता है | * '<math>b</math>' अर्ध-लघु अक्ष (लघु अक्ष की लंबाई का आधा) को दर्शाता है | ||
== दीर्घवृत्त के भाग == | == दीर्घवृत्त के भाग == | ||
आइए दीर्घवृत्त के विभिन्न भागों से संबंधित कुछ महत्वपूर्ण शब्दों पर | आइए दीर्घवृत्त के विभिन्न भागों से संबंधित कुछ महत्वपूर्ण शब्दों पर दृष्टि डालें। | ||
'''नाभि''': दीर्घवृत्त में दो नाभियाँ होती हैं और उनके निर्देशांक <math>F(c, o)</math>, और <math>F'(-c, 0)</math> होते हैं। इस प्रकार नाभियों के बीच की दूरी <math>2c</math> के बराबर होती है। | |||
केंद्र: दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को दीर्घवृत्त का केंद्र कहा जाता है। इसे (h, k) द्वारा दर्शाया जाता है। | '''केंद्र''': दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को दीर्घवृत्त का केंद्र कहा जाता है। इसे <math>(h, k)</math> द्वारा दर्शाया जाता है। | ||
'''दीर्घ अक्ष''': दीर्घ अक्ष दीर्घवृत्त का सबसे लंबा व्यास होता है। दीर्घवृत्त के दीर्घ अक्ष की लंबाई <math>2a</math> इकाई होती है, और इस दीर्घ अक्ष के अंतिम कोने क्रमशः <math>(a, 0), (-a, 0)</math> होते हैं। | |||
लघु अक्ष: लघु अक्ष दीर्घवृत्त का सबसे छोटा व्यास होता है। दीर्घवृत्त के लघु अक्ष की लंबाई 2b इकाई होती है और लघु अक्ष के अंतिम कोने क्रमशः (0, b), और (0, -b) होते हैं। | '''लघु अक्ष''': लघु अक्ष दीर्घवृत्त का सबसे छोटा व्यास होता है। दीर्घवृत्त के लघु अक्ष की लंबाई <math>2b</math> इकाई होती है और लघु अक्ष के अंतिम कोने क्रमशः <math>(0, b),</math> और <math>(0, -b)</math> होते हैं। | ||
अनुप्रस्थ अक्ष: दीर्घवृत्त के दो फोकस और केंद्र से गुजरने वाली रेखा को अनुप्रस्थ अक्ष कहा जाता है। | '''अनुप्रस्थ अक्ष''': दीर्घवृत्त के दो फोकस और केंद्र से गुजरने वाली रेखा को अनुप्रस्थ अक्ष कहा जाता है। | ||
'''नाभिलंब जीवा''': लेटस रेक्टम दीर्घवृत्त के अनुप्रस्थ अक्ष के लंबवत खींची गई रेखा है और दीर्घवृत्त के फोकस से होकर गुजर रही है। दीर्घवृत्त के लेटस रेक्टम की लंबाई <math>\frac{2 b^2}{a}</math> है। | |||
'''संयुग्मी अक्ष''': दीर्घवृत्त के केंद्र से गुजरने वाली और अनुप्रस्थ अक्ष के लंबवत रेखा को संयुग्मी अक्ष कहा जाता है | |||
उत्केन्द्रता: (e < 1)। दीर्घवृत्त के केंद्र से फोकस की दूरी और दीर्घवृत्त के केंद्र से | '''उत्केन्द्रता''':<math>(e < 1)</math>। दीर्घवृत्त के केंद्र से फोकस की दूरी और दीर्घवृत्त के केंद्र से दीर्घ अक्ष के एक छोर की दूरी का अनुपात। यदि दीर्घवृत्त के केंद्र से फोकस की दूरी '<math>c</math>' है और केंद्र से दीर्घ अक्ष के अंत की दूरी '<math>a</math>' है, तो उत्केन्द्रता <math>e =\frac{c}{a}</math>. | ||
[[File:दीर्घवृत्त - शंकु परिच्छेद.jpg|thumb|276x276px|चित्र दीर्घवृत्त - शंकु परिच्छेद]] | |||
== दीर्घवृत्त - शंकु परिच्छेद == | == दीर्घवृत्त - शंकु परिच्छेद == | ||
दीर्घवृत्त एक शंकु | दीर्घवृत्त एक शंकु परिच्छेद है, जो तब बनता है जब एक समतल शंकु को एक कोण पर काटता है। दीर्घवृत्त में 2 नाभियाँ, एक दीर्घ अक्ष और एक लघु अक्ष होता है। दीर्घवृत्त के लिए उत्केन्द्रता <math>(e)</math> का मान <math>(e < 1)</math> है। दीर्घवृत्त में 2 दिशाएँ होती हैं।<math>(h, k)</math> पर केंद्र और दीर्घ और लघु अक्षों की लंबाई क्रमशः '<math>2a</math>' और '<math>2b</math>' के साथ दीर्घवृत्त के समीकरण का सामान्य रूप। दीर्घवृत्त की प्रमुख धुरी <math>x </math>-अक्ष के समानांतर होती है। दीर्घवृत्त के लिए शंकु परिच्छेद सूत्र इस प्रकार है। | ||
( | <math>\frac{(x-h)^2}{a^2} +\frac{ (y-k)^2}{b^2} = 1</math> | ||
'''टिप्पणी''' : यदि दीर्घ अक्ष <math>y </math>-अक्ष के समान्तर है, तो ऊपर दिए गए सूत्र में <math>a </math> और <math>b </math> के स्थान बदलें। | |||
टिप्पणी : यदि दीर्घ अक्ष y-अक्ष के समान्तर है, तो ऊपर दिए गए सूत्र में a और b के स्थान बदलें। | |||
== दीर्घवृत्त का मानक समीकरण == | == दीर्घवृत्त का मानक समीकरण == | ||
दीर्घवृत्त के दो मानक समीकरण हैं। ये समीकरण प्रत्येक दीर्घवृत्त के अनुप्रस्थ अक्ष और संयुग्म अक्ष पर आधारित हैं। | दीर्घवृत्त के दो मानक समीकरण हैं। ये समीकरण प्रत्येक दीर्घवृत्त के अनुप्रस्थ अक्ष और संयुग्म अक्ष पर आधारित हैं। | ||
* दीर्घवृत्त के मानक समीकरण | * दीर्घवृत्त के मानक समीकरण <math>\frac{x^2}{ a^2}+\frac{y^2 }{ b^2}=1</math> में अनुप्रस्थ अक्ष <math>x </math>-अक्ष और संयुग्मी अक्ष <math>y </math>-अक्ष है। | ||
* एक अन्य दीर्घवृत्त मानक रूप | * एक अन्य दीर्घवृत्त मानक रूप <math>\frac{x^2}{ b^2}+\frac{y^2 }{ a^2}=1</math> है और इसमें अनुप्रस्थ अक्ष <math>y </math>-अक्ष के रूप में और इसका संयुग्मी अक्ष <math>x </math>-अक्ष के रूप में है। | ||
नीचे दी गई छवि दीर्घवृत्त के दो मानक रूपों को दर्शाती है। | नीचे दी गई छवि दीर्घवृत्त के दो मानक रूपों को दर्शाती है। | ||
== दीर्घवृत्त के गुणधर्म == | == दीर्घवृत्त के गुणधर्म == | ||
ऐसे कई गुण हैं जो दीर्घवृत्त को अन्य समान आकृतियों से अलग करने में | ऐसे कई गुण हैं जो दीर्घवृत्त को अन्य समान आकृतियों से अलग करने में सहायता करते हैं। दीर्घवृत्त के ये गुणधर्म इस प्रकार दिए गए हैं, | ||
एक दीर्घवृत्त का उत्केन्द्रता मान | * एक दीर्घवृत्त, शंकु को उसके आधार के कोण पर प्रतिच्छेद करने वाले समतल द्वारा बनाया जाता है। | ||
* सभी दीर्घवृत्तों में दो नाभि या केन्द्र बिंदु(फ़ोकल पॉइंट) होते हैं। दीर्घवृत्त पर किसी भी बिंदु से दो फ़ोकल पॉइंट तक की दूरी का योग एक स्थिर मान होता है। | |||
* एक दीर्घवृत्त में एक केंद्र और एक दीर्घ और लघु अक्ष होता है। | |||
* एक दीर्घवृत्त का उत्केन्द्रता मान <math>1 </math> से कम होता है। | |||
[[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]] | ||
Latest revision as of 11:25, 22 November 2024
दीर्घवृत्त शंकु परिच्छेद का एक अभिन्न अंग है और गुणों में वृत्त के समान है। वृत्त के विपरीत, दीर्घवृत्त आकार में अंडाकार होता है। दीर्घवृत्त की उत्केन्द्रता एक से कम होती है, और यह बिंदुओं के बिन्दुपथ को दर्शाता है, जिनकी दो नाभियों से दूरियों का योग एक स्थिर मान होता है। हमारे दैनिक जीवन में दीर्घवृत्त के सरल उदाहरण दो-आयामी रूप में अंडे का आकार, खेल स्टेडियम में दौड़ना आदि हैं।
यहाँ हम दीर्घवृत्त की परिभाषा, दीर्घवृत्त के समीकरण की व्युत्पत्ति और दीर्घवृत्त के समीकरणों के विभिन्न मानक रूपों को जानने का लक्ष्य रखेंगे।
परिचय
गणित में, दीर्घवृत्त एक संवृत वक्र होता है जो दो लंबवत अक्षों के संबंध में सममित होता है। इसे एक समतल में सभी बिंदुओं के समूह के रूप में परिभाषित किया जा सकता है, जैसे कि वक्र पर किसी भी बिंदु से दो निश्चित बिंदुओं (जिन्हें नाभि(फोकस)कहा जाता है) तक की दूरी का योग स्थिर होता है। निश्चित बिंदुओं को नाभि कहा जाता है और उन्हें और द्वारा दर्शाया जाता है।
दीर्घवृत्त शंकु वर्गों में से एक है, जो शंकु का उस समतल से प्रतिच्छेदन है जो शंकु के आधार को प्रतिच्छेद नहीं करता है।
परिभाषा
दीर्घवृत्त एक समतल में स्थित बिंदुओं का बिन्दुपथ है, जिसकी दो स्थिर बिंदुओं से दूरियों का योग एक स्थिर मान होता है। दो स्थिर बिंदुओं को दीर्घवृत्त की नाभियाँ कहते हैं।
दीर्घवृत्त समीकरण
दीर्घवृत्त के सामान्य समीकरण का उपयोग निर्देशांक तल में दीर्घवृत्त को बीजगणितीय रूप से दर्शाने के लिए किया जाता है। दीर्घवृत्त का समीकरण इस प्रकार दिया जा सकता है,
, जहाँ
- '' अर्ध-दीर्घ अक्ष (दीर्घ अक्ष की लंबाई का आधा) को दर्शाता है
- '' अर्ध-लघु अक्ष (लघु अक्ष की लंबाई का आधा) को दर्शाता है
दीर्घवृत्त के भाग
आइए दीर्घवृत्त के विभिन्न भागों से संबंधित कुछ महत्वपूर्ण शब्दों पर दृष्टि डालें।
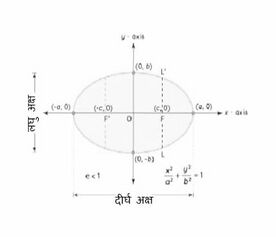
नाभि: दीर्घवृत्त में दो नाभियाँ होती हैं और उनके निर्देशांक , और होते हैं। इस प्रकार नाभियों के बीच की दूरी के बराबर होती है।
केंद्र: दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को दीर्घवृत्त का केंद्र कहा जाता है। इसे द्वारा दर्शाया जाता है।
दीर्घ अक्ष: दीर्घ अक्ष दीर्घवृत्त का सबसे लंबा व्यास होता है। दीर्घवृत्त के दीर्घ अक्ष की लंबाई इकाई होती है, और इस दीर्घ अक्ष के अंतिम कोने क्रमशः होते हैं।
लघु अक्ष: लघु अक्ष दीर्घवृत्त का सबसे छोटा व्यास होता है। दीर्घवृत्त के लघु अक्ष की लंबाई इकाई होती है और लघु अक्ष के अंतिम कोने क्रमशः और होते हैं।
अनुप्रस्थ अक्ष: दीर्घवृत्त के दो फोकस और केंद्र से गुजरने वाली रेखा को अनुप्रस्थ अक्ष कहा जाता है।
नाभिलंब जीवा: लेटस रेक्टम दीर्घवृत्त के अनुप्रस्थ अक्ष के लंबवत खींची गई रेखा है और दीर्घवृत्त के फोकस से होकर गुजर रही है। दीर्घवृत्त के लेटस रेक्टम की लंबाई है।
संयुग्मी अक्ष: दीर्घवृत्त के केंद्र से गुजरने वाली और अनुप्रस्थ अक्ष के लंबवत रेखा को संयुग्मी अक्ष कहा जाता है
उत्केन्द्रता:। दीर्घवृत्त के केंद्र से फोकस की दूरी और दीर्घवृत्त के केंद्र से दीर्घ अक्ष के एक छोर की दूरी का अनुपात। यदि दीर्घवृत्त के केंद्र से फोकस की दूरी '' है और केंद्र से दीर्घ अक्ष के अंत की दूरी '' है, तो उत्केन्द्रता .
दीर्घवृत्त - शंकु परिच्छेद
दीर्घवृत्त एक शंकु परिच्छेद है, जो तब बनता है जब एक समतल शंकु को एक कोण पर काटता है। दीर्घवृत्त में 2 नाभियाँ, एक दीर्घ अक्ष और एक लघु अक्ष होता है। दीर्घवृत्त के लिए उत्केन्द्रता का मान है। दीर्घवृत्त में 2 दिशाएँ होती हैं। पर केंद्र और दीर्घ और लघु अक्षों की लंबाई क्रमशः '' और '' के साथ दीर्घवृत्त के समीकरण का सामान्य रूप। दीर्घवृत्त की प्रमुख धुरी -अक्ष के समानांतर होती है। दीर्घवृत्त के लिए शंकु परिच्छेद सूत्र इस प्रकार है।
टिप्पणी : यदि दीर्घ अक्ष -अक्ष के समान्तर है, तो ऊपर दिए गए सूत्र में और के स्थान बदलें।
दीर्घवृत्त का मानक समीकरण
दीर्घवृत्त के दो मानक समीकरण हैं। ये समीकरण प्रत्येक दीर्घवृत्त के अनुप्रस्थ अक्ष और संयुग्म अक्ष पर आधारित हैं।
- दीर्घवृत्त के मानक समीकरण में अनुप्रस्थ अक्ष -अक्ष और संयुग्मी अक्ष -अक्ष है।
- एक अन्य दीर्घवृत्त मानक रूप है और इसमें अनुप्रस्थ अक्ष -अक्ष के रूप में और इसका संयुग्मी अक्ष -अक्ष के रूप में है।
नीचे दी गई छवि दीर्घवृत्त के दो मानक रूपों को दर्शाती है।
दीर्घवृत्त के गुणधर्म
ऐसे कई गुण हैं जो दीर्घवृत्त को अन्य समान आकृतियों से अलग करने में सहायता करते हैं। दीर्घवृत्त के ये गुणधर्म इस प्रकार दिए गए हैं,
- एक दीर्घवृत्त, शंकु को उसके आधार के कोण पर प्रतिच्छेद करने वाले समतल द्वारा बनाया जाता है।
- सभी दीर्घवृत्तों में दो नाभि या केन्द्र बिंदु(फ़ोकल पॉइंट) होते हैं। दीर्घवृत्त पर किसी भी बिंदु से दो फ़ोकल पॉइंट तक की दूरी का योग एक स्थिर मान होता है।
- एक दीर्घवृत्त में एक केंद्र और एक दीर्घ और लघु अक्ष होता है।
- एक दीर्घवृत्त का उत्केन्द्रता मान से कम होता है।