अतिपरवलय: Difference between revisions

Latest revision as of 17:41, 22 November 2024

गणित में, अतिपरवलय एक महत्वपूर्ण शंकु खंड है जो एक समतल सतह द्वारा दोहरे शंकु के प्रतिच्छेदन द्वारा बनता है, लेकिन जरूरी नहीं कि केंद्र में हो। अतिपरवलय संयुग्मी अक्ष के साथ सममित होता है, और दीर्घवृत्त के साथ कई समानताएँ साझा करता है। नाभि(फोकस), नियता(डायरेक्ट्रिक्स), नाभिलंब जीवा(लैटस रेक्टम) और उत्केन्द्रता(एक्सेंट्रिकिटी) जैसी अवधारणाएँ अतिपरवलय पर लागू होती हैं। अतिपरवलय के कुछ सामान्य उदाहरणों में सूर्यघड़ी की छाया की नोक द्वारा अनुसरण किया जाने वाला पथ, उप-परमाणु कणों का प्रकीर्णन पथ आदि उपस्थित हैं।

यहाँ हम हल किए गए उदाहरणों का उपयोग करके अतिपरवलय की परिभाषा, सूत्र, सूत्र की व्युत्पत्ति और अतिपरवलय के मानक रूपों को समझने का लक्ष्य रखेंगे।

परिचय

अतिपरवलय , समतल में प्रसूत एक प्रकार का चिकना वक्र होता है, जिसमें दो टुकड़े होते हैं, जिन्हें जुड़े हुए घटक या शाखाएँ कहते हैं, जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं और दो अनंत धनुषों के समान होते हैं। अतिपरवलय बिंदुओं का एक समूह होता है, जिनकी दो नाभियों से दूरी का अंतर एक स्थिर मान होता है। यह अंतर दूर के नाभियों से दूरी और फिर समीप की नाभियों से दूरी से लि जाती है। अतिपरवलय पर एक बिंदु $P(x,y)$ और दो नाभियों $F$ , $F'$ के लिए, अतिपरवलय का स्थान $PF-PF'=2a$ है।

परिभाषा

विश्लेषणात्मक ज्यामिति में अतिपरवलय एक शंकु खंड है जो तब बनता है जब एक समतल एक दोहरे समकोणीय वृत्ताकार शंकु को इस तरह के कोण पर काटता है कि शंकु के दोनों हिस्से एक दूसरे को काटते हैं। समतल और शंकु के इस प्रतिच्छेदन से दो अलग-अलग असीमित वक्र बनते हैं जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं जिन्हें अतिपरवलय कहा जाता है।

चित्र- अतिपरवलय - शंकु के परिच्छेद

अतिपरवलय - शंकु के परिच्छेद

अतिपरवलय तब बनता है जब प्रभावशाली समतल शंकु की धुरी के समानांतर होता है, और दोहरे शंकु के दोनों नैप्स के साथ प्रतिच्छेद करता है। अतिपरवलय के लिए उत्केन्द्रता $(e)$ का मान $e<1$ है। अतिपरवलय के दो असंबद्ध खंडों को शाखाएँ कहा जाता है। वे एक दूसरे के दर्पण प्रतिबिम्ब हैं, और उनकी तिरछी विपरीत भुजाएँ एक रेखा की सीमा तक पहुँचती हैं।

अतिपरवलय एक शंकु के परिच्छेद का एक उदाहरण है जिसे एक समतल पर खींचा जा सकता है जो दो नैप्स से बने दोहरे शंकु को प्रतिच्छेद करता है। $(h,k)$ को केंद्र मानकर अतिपरवलय के समीकरण का सामान्य रूप इस प्रकार है।

${\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1$

अतिपरवलय के भाग

आइए अतिपरवलय के विभिन्न मापदंडों से संबंधित कुछ महत्वपूर्ण शब्दों की जाँच करें।

अतिपरवलय के नाभियाँ: अतिपरवलय के दो नाभियाँ होती हैं और उनके निर्देशांक $F(c,o),$ और $F'(-c,0)$ होते हैं।

अतिपरवलय का केंद्र: दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को अतिपरवलय का केंद्र कहा जाता है।

दीर्घ अक्ष: अतिपरवलय के दीर्घ अक्ष की लंबाई $2a$ इकाई होती है।

लघु अक्ष: अतिपरवलय के लघु अक्ष की लंबाई $2b$ इकाई होती है।

शीर्ष: वे बिंदु जहाँ अतिपरवलय अक्ष से गुजरता है, शीर्ष कहलाते हैं। अतिपरवलय के शीर्ष $(a,0),(-a,0)$ हैं।

अतिपरवलय का नाभिलंब जीवा: नाभिलंब जीवा अतिपरवलय की अनुप्रस्थ अक्ष के लंबवत खींची गई एक रेखा है और अतिपरवलय के नाभियों से होकर गुज़रती है। अतिपरवलय के नाभिलंब जीवा की लंबाई ${\frac {2b^{2}}{a}}$ है।

अनुप्रस्थ अक्ष: अतिपरवलय के दो नाभियों और केंद्र से गुजरने वाली रेखा को अतिपरवलय का अनुप्रस्थ अक्ष कहा जाता है।

संयुग्मी अक्ष: अतिपरवलय के केंद्र से गुजरने वाली और अनुप्रस्थ अक्ष के लंबवत रेखा को अतिपरवलय का संयुग्मी अक्ष कहा जाता है।

अतिपरवलय की उत्केन्द्रता: $(e<1)$ उत्केन्द्रता अतिपरवलय के केंद्र से नाभियों की दूरी और अतिपरवलय के केंद्र से शीर्ष की दूरी का अनुपात है। नाभियों की दूरी ' $c$ ' इकाई है, और शीर्ष की दूरी ' $a$ ' इकाई है, और इसलिए उत्केन्द्रता $e={\frac {c}{a}}$ है।

अतिपरवलय समीकरण

नीचे दिया गया समीकरण अतिपरवलय के सामान्य समीकरण को दर्शाता है। यहाँ $x$ -अक्ष अतिपरवलय का अनुप्रस्थ अक्ष है, और $y$ -अक्ष अतिपरवलय का संयुग्मी अक्ष है।

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

चित्र-अतिपरवलय का मानक समीकरण

अतिपरवलय का मानक समीकरण

अतिपरवलय के दो मानक समीकरण हैं। ये समीकरण प्रत्येक अतिपरवलय के अनुप्रस्थ अक्ष और संयुग्मी अक्ष पर आधारित हैं। अतिपरवलय का मानक समीकरण है

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

जिसमें अनुप्रस्थ अक्ष $x$ -अक्ष है और संयुग्मी अक्ष $y$ -अक्ष है। इसके अलावा, अतिपरवलय का एक और मानक समीकरण है

${\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1$

और इसमें अनुप्रस्थ अक्ष $y$ -अक्ष है और इसका संयुग्मी अक्ष $x$ -अक्ष है। ऊपर दी गई छवि अतिपरवलय के समीकरणों के दो मानक रूपों को दिखाती है।

उदाहरण: अतिपरवलय का समीकरण इस प्रकार दिया गया है: ${\frac {(x-5)^{2}}{4^{2}}}-{\frac {(y-2)^{2}}{2^{2}}}=1$ अतिपरवलय सूत्रों का उपयोग करके दीर्घ अक्ष और लघु अक्ष की लंबाई ज्ञात करें।

समाधान:

दीर्घ और लघु अक्ष की लंबाई के लिए अतिपरवलय सूत्र का उपयोग करना

दीर्घ अक्ष की लंबाई $=2a,$ और लघु अक्ष की लंबाई $=2b$

दीर्घ अक्ष की लंबाई $=2\times 4=8,$ और लघु अक्ष की लंबाई $=2\times 2=4$

अतिपरवलय के गुणधर्म

विभिन्न अवधारणाओं से संबंधित निम्नलिखित महत्वपूर्ण गुण अतिपरवलय को बेहतर ढंग से समझने में मदद करते हैं।

अनंतस्पर्शी(असिम्प्टोट): अतिपरवलय के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर अतिपरवलय को छूती हैं। अतिपरवलय के अनंतस्पर्शी के समीकरण क्रमशः $y={\frac {bx}{a}},$ और $y={\frac {-bx}{a}}$ हैं।

आयताकार अतिपरवलय: अनुप्रस्थ अक्ष और संयुग्मी अक्ष की समान लंबाई वाले अतिपरवलय को आयताकार अतिपरवलय कहते हैं। यहाँ, हमारे पास $2a=2b,$ या $a=b$ है। इसलिए आयताकार अतिपरवलय का समीकरण $x^{2}-y^{2}=a^{2}$ के बराबर है

पैरामीट्रिक निर्देशांक: अतिपरवलय पर बिंदुओं को पैरामीट्रिक निर्देशांक $(x,y)=(asec\theta ,btan\theta )$ के साथ दर्शाया जा सकता है। अतिपरवलय पर बिंदुओं को दर्शाने वाले ये पैरामीट्रिक निर्देशांक अतिपरवलय के समीकरण को संतुष्ट करते हैं।

सहायक वृत्त: अतिपरवलय के अनुप्रस्थ अक्ष के अंत बिंदुओं को इसके व्यास के रूप में लेकर खींचा गया वृत्त सहायक वृत्त कहलाता है। अतिपरवलय के सहायक वृत्त का समीकरण $x^{2}+y^{2}=a^{2}$ है।

दिशा वृत्त: अतिपरवलय पर लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निर्देशक वृत्त कहते हैं। अतिपरवलय के निर्देशक वृत्त का समीकरण $x^{2}+y^{2}=a^{2}-b^{2}$ है।

@@ Line 1: / Line 1: @@
-गणित में, हाइपरबोला एक महत्वपूर्ण शंकु खंड है जो एक समतल सतह द्वारा दोहरे शंकु के प्रतिच्छेदन द्वारा बनता है, लेकिन जरूरी नहीं कि केंद्र में हो। हाइपरबोला संयुग्म अक्ष के साथ सममित होता है, और दीर्घवृत्त के साथ कई समानताएँ साझा करता है। फ़ोकस, डायरेक्ट्रिक्स, लैटस रेक्टम और एक्सेंट्रिकिटी जैसी अवधारणाएँ हाइपरबोला पर लागू होती हैं। हाइपरबोला के कुछ सामान्य उदाहरणों में सूर्यघड़ी की छाया की नोक द्वारा अनुसरण किया जाने वाला पथ, उप-परमाणु कणों का प्रकीर्णन पथ आदि शामिल हैं।
+गणित में, अतिपरवलय एक महत्वपूर्ण शंकु खंड है जो एक समतल सतह द्वारा दोहरे शंकु के प्रतिच्छेदन द्वारा बनता है, लेकिन जरूरी नहीं कि केंद्र में हो। अतिपरवलय  संयुग्मी  अक्ष के साथ सममित होता है, और दीर्घवृत्त के साथ कई समानताएँ साझा करता है। नाभि(फोकस), नियता(डायरेक्ट्रिक्स), [[नाभिलंब जीवा]](लैटस रेक्टम) और [[उत्केन्द्रता]](एक्सेंट्रिकिटी) जैसी अवधारणाएँ अतिपरवलय  पर लागू होती हैं। अतिपरवलय  के कुछ सामान्य उदाहरणों में सूर्यघड़ी की छाया की नोक द्वारा अनुसरण किया जाने वाला पथ, उप-परमाणु कणों का प्रकीर्णन पथ आदि उपस्थित हैं।
-यहाँ हम हल किए गए उदाहरणों का उपयोग करके हाइपरबोला की परिभाषा, सूत्र, सूत्र की व्युत्पत्ति और हाइपरबोला के मानक रूपों को समझने का लक्ष्य रखेंगे।
+यहाँ हम हल किए गए उदाहरणों का उपयोग करके अतिपरवलय  की परिभाषा, सूत्र, सूत्र की व्युत्पत्ति और अतिपरवलय  के मानक रूपों को समझने का लक्ष्य रखेंगे।
 == परिचय ==
-हाइपरबोला, समतल में पड़ा एक प्रकार का चिकना वक्र होता है, जिसमें दो टुकड़े होते हैं, जिन्हें जुड़े हुए घटक या शाखाएँ कहते हैं, जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं और दो अनंत धनुषों के समान होते हैं। हाइपरबोला बिंदुओं का एक समूह होता है, जिनकी दो फ़ोकस से दूरी का अंतर एक स्थिर मान होता है। यह अंतर दूर के फ़ोकस से दूरी और फिर नज़दीकी फ़ोकस से दूरी से लिया जाता है। हाइपरबोला पर एक बिंदु P(x, y) और दो फ़ोकस F, F' के लिए, हाइपरबोला का स्थान PF - PF' = 2a है।
+अतिपरवलय , समतल में प्रसूत एक प्रकार का चिकना वक्र होता है, जिसमें दो टुकड़े होते हैं, जिन्हें जुड़े हुए घटक या शाखाएँ कहते हैं, जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं और दो अनंत धनुषों के समान होते हैं। अतिपरवलय  बिंदुओं का एक समूह होता है, जिनकी दो नाभियों से दूरी का अंतर एक स्थिर मान होता है। यह अंतर दूर के नाभियों से दूरी और फिर समीप की नाभियों से दूरी से लि जाती है। अतिपरवलय  पर एक बिंदु <math>P(x, y)</math> और दो नाभियों <math>F</math>, <math>F'</math> के लिए, अतिपरवलय  का स्थान <math>PF - PF' = 2a</math> है।
 == परिभाषा ==
-विश्लेषणात्मक ज्यामिति में हाइपरबोला एक शंकु खंड है जो तब बनता है जब एक समतल एक दोहरे समकोणीय वृत्ताकार शंकु को इस तरह के कोण पर काटता है कि शंकु के दोनों हिस्से एक दूसरे को काटते हैं। समतल और शंकु के इस प्रतिच्छेदन से दो अलग-अलग असीमित वक्र बनते हैं जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं जिन्हें हाइपरबोला कहा जाता है।
+विश्लेषणात्मक ज्यामिति में अतिपरवलय  एक शंकु खंड है जो तब बनता है जब एक समतल एक दोहरे समकोणीय वृत्ताकार शंकु को इस तरह के कोण पर काटता है कि शंकु के दोनों हिस्से एक दूसरे को काटते हैं। समतल और शंकु के इस प्रतिच्छेदन से दो अलग-अलग असीमित वक्र बनते हैं जो एक दूसरे के दर्पण प्रतिबिम्ब होते हैं जिन्हें अतिपरवलय  कहा जाता है।
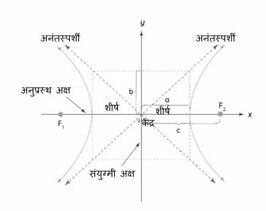
+[[File:अतिपरवलय - शंकु के परिच्छेद.jpg|thumb|266x266px|चित्र- अतिपरवलय  - शंकु के परिच्छेद]]
-== हाइपरबोला - शंकु खंड ==
+== अतिपरवलय  - शंकु के परिच्छेद ==
-हाइपरबोला तब बनता है जब दिलचस्प समतल शंकु की धुरी के समानांतर होता है, और दोहरे शंकु के दोनों नैप्स के साथ प्रतिच्छेद करता है। हाइपरबोला के लिए उत्केन्द्रता <math>(e)</math> का मान <math>e < 1</math> है। हाइपरबोला के दो असंबद्ध खंडों को शाखाएँ कहा जाता है। वे एक दूसरे के दर्पण प्रतिबिम्ब हैं, और उनकी तिरछी विपरीत भुजाएँ एक रेखा की सीमा तक पहुँचती हैं।
+अतिपरवलय  तब बनता है जब प्रभावशाली समतल शंकु की धुरी के समानांतर होता है, और दोहरे शंकु के दोनों नैप्स के साथ प्रतिच्छेद करता है। अतिपरवलय  के लिए उत्केन्द्रता <math>(e)</math> का मान <math>e < 1</math> है। अतिपरवलय  के दो असंबद्ध खंडों को शाखाएँ कहा जाता है। वे एक दूसरे के दर्पण प्रतिबिम्ब हैं, और उनकी तिरछी विपरीत भुजाएँ एक रेखा की सीमा तक पहुँचती हैं।
-हाइपरबोला एक शंकु खंड का एक उदाहरण है जिसे एक समतल पर खींचा जा सकता है जो दो नैप्स से बने दोहरे शंकु को प्रतिच्छेद करता है। <math>(h, k)</math> को केंद्र मानकर हाइपरबोला के समीकरण का सामान्य रूप इस प्रकार है।
+अतिपरवलय  एक शंकु के परिच्छेद का एक उदाहरण है जिसे एक समतल पर खींचा जा सकता है जो दो नैप्स से बने दोहरे शंकु को प्रतिच्छेद करता है। <math>(h, k)</math> को केंद्र मानकर अतिपरवलय  के समीकरण का सामान्य रूप इस प्रकार है।
-(x−h)2/a2 - (y−k)2/b2 = 1
+<math>\frac{(x-h)^2}{a^2} -\frac{ (y-k)^2}{b^2} = 1</math>
-== हाइपरबोला के भाग ==
+== अतिपरवलय  के भाग ==
-आइए हाइपरबोला के विभिन्न मापदंडों से संबंधित कुछ महत्वपूर्ण शब्दों की जाँच करें।
+आइए अतिपरवलय  के विभिन्न मापदंडों से संबंधित कुछ महत्वपूर्ण शब्दों की जाँच करें।
-हाइपरबोला के नाभियाँ: हाइपरबोला के दो नाभियाँ होती हैं और उनके निर्देशांक F(c, o), और F'(-c, 0) होते हैं।
+'''अतिपरवलय  के नाभियाँ''': अतिपरवलय  के दो नाभियाँ होती हैं और उनके निर्देशांक <math>F(c, o),</math> और <math>F'(-c, 0)</math> होते हैं।
-हाइपरबोला का केंद्र: दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को हाइपरबोला का केंद्र कहा जाता है।
+'''अतिपरवलय  का केंद्र''': दो नाभियों को मिलाने वाली रेखा के मध्यबिंदु को अतिपरवलय  का केंद्र कहा जाता है।
-दीर्घ अक्ष: हाइपरबोला के दीर्घ अक्ष की लंबाई 2a इकाई होती है।
+'''दीर्घ अक्ष''': अतिपरवलय के दीर्घ अक्ष की लंबाई <math>2a</math> इकाई होती है।
-लघु अक्ष: हाइपरबोला के लघु अक्ष की लंबाई 2b इकाई होती है।
+'''लघु अक्ष''': अतिपरवलय के लघु अक्ष की लंबाई <math>2b</math> इकाई होती है।
-शीर्ष: वे बिंदु जहाँ हाइपरबोला अक्ष को काटता है, शीर्ष कहलाते हैं। हाइपरबोला के शीर्ष (a, 0), (-a, 0) हैं।
+'''शीर्ष''': वे बिंदु जहाँ अतिपरवलय अक्ष से गुजरता है, शीर्ष कहलाते हैं। अतिपरवलय  के शीर्ष <math>(a, 0), (-a, 0)</math> हैं।
-हाइपरबोला का लेटस रेक्टम: लेटस रेक्टम हाइपरबोला की अनुप्रस्थ अक्ष के लंबवत खींची गई एक रेखा है और हाइपरबोला के नाभियों से होकर गुज़रती है। हाइपरबोला के लेटस रेक्टम की लंबाई 2b2/a है।
+'''अतिपरवलय  का नाभिलंब जीवा''': नाभिलंब जीवा अतिपरवलय  की अनुप्रस्थ अक्ष के लंबवत खींची गई एक रेखा है और अतिपरवलय  के नाभियों से होकर गुज़रती है। अतिपरवलय  के नाभिलंब जीवा की लंबाई <math>\frac{2 b^2}{a}</math> है।
-अनुप्रस्थ अक्ष: हाइपरबोला के दो फोकस और केंद्र से गुजरने वाली रेखा को हाइपरबोला का अनुप्रस्थ अक्ष कहा जाता है।
+'''अनुप्रस्थ अक्ष''': अतिपरवलय  के दो नाभियों और केंद्र से गुजरने वाली रेखा को अतिपरवलय  का अनुप्रस्थ अक्ष कहा जाता है।
-संयुग्म अक्ष: हाइपरबोला के केंद्र से गुजरने वाली और अनुप्रस्थ अक्ष के लंबवत रेखा को हाइपरबोला का संयुग्म अक्ष कहा जाता है।
+'''संयुग्मी अक्ष''': अतिपरवलय  के केंद्र से गुजरने वाली और अनुप्रस्थ अक्ष के लंबवत रेखा को अतिपरवलय का संयुग्मी अक्ष कहा जाता है।
-हाइपरबोला की उत्केन्द्रता: (e > 1) उत्केन्द्रता हाइपरबोला के केंद्र से फोकस की दूरी और हाइपरबोला के केंद्र से शीर्ष की दूरी का अनुपात है। फोकस की दूरी 'c' इकाई है, और शीर्ष की दूरी 'a' इकाई है, और इसलिए उत्केन्द्रता e = c/a है।
+'''अतिपरवलय  की उत्केन्द्रता''': <math>(e < 1)</math>  उत्केन्द्रता अतिपरवलय  के केंद्र से नाभियों की दूरी और अतिपरवलय  के केंद्र से शीर्ष की दूरी का अनुपात है। नाभियों की दूरी '<math>c</math>' इकाई है, और शीर्ष की दूरी '<math>a</math>' इकाई है, और इसलिए उत्केन्द्रता <math>e =\frac{c}{a}</math> है।
-== हाइपरबोला समीकरण ==
+== अतिपरवलय  समीकरण ==
-नीचे दिया गया समीकरण हाइपरबोला के सामान्य समीकरण को दर्शाता है। यहाँ x-अक्ष हाइपरबोला का अनुप्रस्थ अक्ष है, और y-अक्ष हाइपरबोला का संयुग्म अक्ष है।
+नीचे दिया गया समीकरण अतिपरवलय  के सामान्य समीकरण को दर्शाता है। यहाँ <math>x</math>-अक्ष अतिपरवलय  का अनुप्रस्थ अक्ष है, और <math>y</math>-अक्ष अतिपरवलय  का संयुग्मी अक्ष है।
-x2a2−y2b2=1
+<math>\frac{x^2}{ a^2}-\frac{y^2 }{ b^2}=1</math>
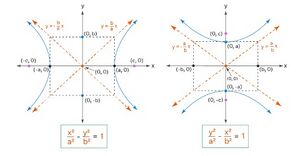
+[[File:अतिपरवलय का मानक समीकरण.jpg|thumb|चित्र-अतिपरवलय का मानक समीकरण]]
-image
+== अतिपरवलय  का मानक समीकरण ==
+अतिपरवलय  के दो मानक समीकरण हैं। ये समीकरण प्रत्येक अतिपरवलय  के अनुप्रस्थ अक्ष और संयुग्मी  अक्ष पर आधारित हैं। अतिपरवलय  का मानक समीकरण है
-आइये हम हाइपरबोला समीकरण के मानक रूप और इसकी व्युत्पत्ति को निम्नलिखित अनुभागों में विस्तार से समझें।
+<math>\frac{x^2}{ a^2}-\frac{y^2 }{ b^2}=1</math>
-== हाइपरबोला का मानक समीकरण ==
+जिसमें अनुप्रस्थ अक्ष <math>x</math>-अक्ष है और संयुग्मी  अक्ष <math>y</math>-अक्ष है। इसके अलावा, अतिपरवलय  का एक और मानक समीकरण है
-हाइपरबोला के दो मानक समीकरण हैं। ये समीकरण प्रत्येक हाइपरबोला के अनुप्रस्थ अक्ष और संयुग्म अक्ष पर आधारित हैं। हाइपरबोला का मानक समीकरण है
-x2a2−y2b2=1
+<math>\frac{y^2}{ a^2}-\frac{x^2 }{ b^2}=1</math>
-जिसमें अनुप्रस्थ अक्ष x-अक्ष है और संयुग्म अक्ष y-अक्ष है। इसके अलावा, हाइपरबोला का एक और मानक समीकरण है
+और इसमें अनुप्रस्थ अक्ष <math>y</math>-अक्ष है और इसका संयुग्मी  अक्ष <math>x</math>-अक्ष है। ऊपर दी गई छवि अतिपरवलय  के समीकरणों के दो मानक रूपों को दिखाती है।
-y2a2−x2b2=1
+'''उदाहरण''': अतिपरवलय  का समीकरण इस प्रकार दिया गया है: <math>\frac{(x - 5)^2}{4^2} - \frac{(y - 2)^2}{2^2}= 1  </math> अतिपरवलय  सूत्रों का उपयोग करके दीर्घ अक्ष और लघु अक्ष की लंबाई ज्ञात करें।
-और इसमें अनुप्रस्थ अक्ष y-अक्ष है और इसका संयुग्म अक्ष x-अक्ष है। नीचे दी गई छवि हाइपरबोला के समीकरणों के दो मानक रूपों को दिखाती है।
+'''समाधान''':
-== उदाहरण ==
+दीर्घ और लघु अक्ष की लंबाई के लिए अतिपरवलय  सूत्र का उपयोग करना
-उदाहरण: हाइपरबोला का समीकरण इस प्रकार दिया गया है: (x - 5)2/42 - (y - 2)2/22 = 1. हाइपरबोला सूत्रों का उपयोग करके दीर्घ अक्ष और लघु अक्ष की लंबाई ज्ञात करें।
-समाधान:
+दीर्घ अक्ष की लंबाई <math>= 2a,</math> और लघु अक्ष की लंबाई <math>= 2b</math>
-दीर्घ और लघु अक्ष की लंबाई के लिए हाइपरबोला सूत्र का उपयोग करना
+दीर्घ अक्ष की लंबाई <math>= 2 \times 4 = 8,</math> और लघु अक्ष की लंबाई <math>= 2 \times 2 = 4</math>
-दीर्घ अक्ष की लंबाई = 2a, और लघु अक्ष की लंबाई = 2b
+== अतिपरवलय  के गुणधर्म ==
+विभिन्न अवधारणाओं से संबंधित निम्नलिखित महत्वपूर्ण गुण अतिपरवलय  को बेहतर ढंग से समझने में मदद करते हैं।
-दीर्घ अक्ष की लंबाई = 2 × 4 = 8, और लघु अक्ष की लंबाई = 2 × 2 = 4
+'''अनंतस्पर्शी'''('''असिम्प्टोट)''': अतिपरवलय  के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर अतिपरवलय  को छूती हैं। अतिपरवलय  के अनंतस्पर्शी के समीकरण क्रमशः <math>y = \frac{bx}{a},</math> और <math>y = \frac{-bx}{a}</math> हैं।
-== हाइपरबोला के गुणधर्म ==
+'''आयताकार अतिपरवलय''': अनुप्रस्थ अक्ष और संयुग्मी अक्ष की समान लंबाई वाले अतिपरवलय को आयताकार अतिपरवलय कहते हैं। यहाँ, हमारे पास <math>2a = 2b,</math> या <math>a = b</math> है। इसलिए आयताकार अतिपरवलय का समीकरण <math>x^2 - y^2 = a^2</math> के बराबर है
-विभिन्न अवधारणाओं से संबंधित निम्नलिखित महत्वपूर्ण गुण हाइपरबोला को बेहतर ढंग से समझने में मदद करते हैं।
-असिम्प्टोट: हाइपरबोला के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर हाइपरबोला को छूती हैं। हाइपरबोला के असिम्प्टोट के समीकरण क्रमशः y = bx/a, और y = -bx/a हैं।
+'''पैरामीट्रिक निर्देशांक''': अतिपरवलय पर बिंदुओं को पैरामीट्रिक निर्देशांक <math>(x,y) = (asec\theta, btan\theta)</math> के साथ दर्शाया जा सकता है। अतिपरवलय पर बिंदुओं को दर्शाने वाले ये पैरामीट्रिक निर्देशांक अतिपरवलय के समीकरण को संतुष्ट करते हैं।
-आयताकार अतिपरवलय: अनुप्रस्थ अक्ष और संयुग्म अक्ष की समान लंबाई वाले अतिपरवलय को आयताकार अतिपरवलय कहते हैं। यहाँ, हमारे पास 2a = 2b, या a = b है। इसलिए आयताकार अतिपरवलय का समीकरण x2 - y2 = a2 के बराबर है
+'''सहायक वृत्त''': अतिपरवलय के अनुप्रस्थ अक्ष के अंत बिंदुओं को इसके व्यास के रूप में लेकर खींचा गया वृत्त सहायक वृत्त कहलाता है। अतिपरवलय के सहायक वृत्त का समीकरण <math>x^2+ y^2 = a^2</math> है।
-पैरामीट्रिक निर्देशांक: अतिपरवलय पर बिंदुओं को पैरामीट्रिक निर्देशांक (x, y) = (asecθ, btanθ) के साथ दर्शाया जा सकता है। अतिपरवलय पर बिंदुओं को दर्शाने वाले ये पैरामीट्रिक निर्देशांक अतिपरवलय के समीकरण को संतुष्ट करते हैं।
+'''दिशा वृत्त''': अतिपरवलय पर लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निर्देशक वृत्त कहते हैं। अतिपरवलय के निर्देशक वृत्त का समीकरण <math>x^2 + y^2 = a^2 - b^2</math> है।
-सहायक वृत्त: अतिपरवलय के अनुप्रस्थ अक्ष के अंत बिंदुओं को इसके व्यास के रूप में लेकर खींचा गया वृत्त सहायक वृत्त कहलाता है। अतिपरवलय के सहायक वृत्त का समीकरण x2 + y2 = a2 है।
-दिशा वृत्त: अतिपरवलय पर लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निर्देशक वृत्त कहते हैं। अतिपरवलय के निर्देशक वृत्त का समीकरण x2 + y2 = a2 - b2 है।
 [[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]]