|
|
| (9 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| इंटीग्रल एक विधि है, जो बड़े पैमाने पर कार्यों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशेष कार्यों के इंटीग्रल पर चर्चा करें जो आम तौर पर गणना के लिए उपयोग किए जाते हैं। इन इंटीग्रल के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फ़ंक्शन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ।
| | समाकलन एक विधि है, जो बड़े पैमाने पर फलनों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशिष्ट [[फलनों के प्रकार|फलनों]] के समाकलन पर चर्चा करें जो साधारणतः गणना के लिए उपयोग किए जाते हैं। इन समाकलन के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फलन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ। |
|
| |
|
| कई महत्वपूर्ण एकीकरण सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशेष कार्यों के समाकलनों पर एक नज़र डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है। | | कई महत्वपूर्ण [[समाकलन की विधियाँ|समाकलन]] सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशिष्ट फलनों के समाकलनों पर एक दृष्टि डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है।[[File:कुछ विशिष्ट फलनों के समाकलन.jpg|thumb|कुछ विशिष्ट फलनों के समाकलन]] |
| | == समाकलन फलनों का प्रमाण == |
| | अब जब आप इन समाकलन फलनों और उनके मूल्यों के बारे में जानते हैं, तो आइए इनमें से प्रत्येक फलन के प्रमाण पर एक दृष्टि डालें। |
|
| |
|
| विशेष कार्यों के समाकलन
| |
|
| |
|
|
| |
|
| | === फलन 1 का समाकलन === |
| | <math>\int dy / (y^2- a^2) = 1/2a \log \left\vert (y- a) / (y + a) \right\vert + C</math> |
|
| |
|
| | जैसा कि आप जानते हैं, |
|
| |
|
| समाकलन कार्यों का प्रमाण
| | <math>1 / (y^2 - a^2) = 1 / (y - a) (y + a)</math> |
|
| |
|
| अब जब आप इन समाकलन कार्यों और उनके मूल्यों के बारे में जानते हैं, तो आइए इनमें से प्रत्येक फ़ंक्शन के प्रमाण पर एक नज़र डालें।
| | इसका समाधान करते हुए, |
|
| |
|
| ∫ dy / (y<sup>2</sup> – a<sup>2</sup>) = 1/2a log |(y – a) / (y + a)| + C
| | <math>= 1/2a(y+a)-(y-a)/(y-a)(y+a)</math> |
|
| |
|
| As you know,
| | इसे और कम करते हुए, |
|
| |
|
| 1 / (y<sup>2</sup> – a<sup>2</sup>) = 1 / (y – a) (y + a)
| | <math>= 1/2a\ 1/(y-a)-1/(y+a)</math> |
|
| |
|
| Solving this,
| | अतः, <math>\int dy / (y^2-a^2) = 1/2a\int dy/(y-a)-\int dy/(y+a)</math> |
|
| |
|
| = 1/2a
| | इसका समाधान करते हुए, |
|
| |
|
| Reducing it further,
| | <math>= 1/2a\log \left\vert (y-a)-\log \right\vert (y+a) + C</math> |
|
| |
|
| = 1/2a
| | अत:, |
|
| |
|
| Therefore, ∫ dy / (y<sup>2</sup> – a<sup>2</sup>) = 1/2a
| | <math>= 1/2a \log \left\vert (y - a) / (y + a) \right\vert + C</math> |
|
| |
|
| Solving this,
| | === फलन 2 का समाकलन === |
| | <math>\int dy / (a^2 -y^2) = 1/2a \log \left\vert (a + y) / (a- y) \right\vert + C</math> |
|
| |
|
| = 1/2a + C
| | जैसा कि आप जानते हैं, |
|
| |
|
| Hence,
| | <math>1 / (a^2- y^2) = 1 / (a - y) (a + y)</math> |
|
| |
|
| = 1/2a log |(y – a) / (y + a)| + C
| | इसका समाधान करते हुए, |
|
| |
|
| # Integral of function 2
| | <math>= 1/2a\ (a+y)+(a-y)/(a-y)(a+y)</math> |
|
| |
|
| ∫ dy / (a<sup>2</sup> – y<sup>2</sup>) = 1/2a log |(a + y) / (a – y)| + C
| | अत:, |
|
| |
|
| As you,
| | <math>= 1/2a\ 1/(a-y)+1/(a+y)</math> |
|
| |
|
| 1 / (a<sup>2</sup> – y<sup>2</sup>) = 1 / (a – y) (a + y)
| | इसलिए, <math>\int dy / (a^2 -y^2) = 1/2a\int dy/(a-y)+\int dy/(a+y)</math> |
|
| |
|
| Solving,
| | जब आप हल करते हैं, |
|
| |
|
| = 1/2a | | <math>= 1/2a-\log \left\vert (a-y)+\log \right\vert (a+y) + C</math> |
|
| |
|
| Hence,
| | अत:, |
|
| |
|
| = 1/2a | | <math>= 1/2a \log \left\vert (a + y) / (a - y) \right\vert + C</math> |
|
| |
|
| Therefore, ∫ dy / (a<sup>2</sup> – y<sup>2</sup>) = 1/2a
| | === फलन 3 का समाकलन === |
| | <math>\int dy / (y^2 + a^2) = 1/a\ tan^{-1} (y/a) + C</math> |
|
| |
|
| When you solve,
| | <math>y = a \ tan\ t</math> रखने पर, आपको <math>dy = a sec^2\ t\ dt</math> प्राप्त होगा। |
|
| |
|
| = 1/2a + C
| | इसलिए, |
|
| |
|
| Hence,
| | <math>\int dy / (y^2 + a^2) = \int [(a \ sec^2\ t \ dt) / (a^2\ tan^2\ t + a^2)]</math> |
|
| |
|
| = 1/2a log |(a + y) / (a – y)| + C
| | इसका समाधान करते हुए, |
|
| |
|
| # Integral of Function 3
| | <math>\int dy / (y^2 + a^2) = 1/a \int dt = t/a + C</math> |
|
| |
|
| ∫ dy / (y<sup>2</sup> + a<sup>2</sup>) = 1/a tan<sup>–1</sup> (y/a) + C
| | <math>t</math> का मान पुनः प्रतिस्थापित करें, |
|
| |
|
| Substitute y = a tan t, so you have dy = a sec<sup>2</sup> t dt.
| | <math>\int dy / (y^2 + a^2) = 1/a\ tan^{-1} (y/a) + C</math> |
|
| |
|
| Therefore,
| | === फलन 4 का समाकलन === |
| | <math>\int dy / \sqrt{(y^2 - a^2)} = \log \left\vert y + \sqrt{ (y^2 - a^2)} \right\vert + C</math> |
|
| |
|
| ∫ dy / (y<sup>2</sup> + a<sup>2</sup>) = ∫ [(a sec<sup>2</sup> t dt) / (a<sup>2</sup> tan<sup>2</sup> t + a<sup>2</sup>)]
| | प्रतिस्थापित <math>y = a\ sec\ t</math> |
|
| |
|
| Solving,
| | इसलिए, <math>dy = a\ sec\ t\ tan\ t \ dt</math> |
|
| |
|
| ∫ dy / (y<sup>2</sup> + a<sup>2</sup>) = 1/a ∫ dt = t/a + C
| | इसलिए, |
|
| |
|
| Re-substitute the value of t,
| | <math>\int dy / \sqrt{(y^2 -a^2)} = \int a\ sec\ t\ tan \ t\ dt / \sqrt{(a^2 sec^2 t - a^2)}</math> |
|
| |
|
| ∫ dy / (y<sup>2</sup> + a<sup>2</sup>) = 1/a tan<sup>–1</sup> (y/a) + C
| | इसका समाधान करते हुए, |
|
| |
|
| # Integral of Function 4
| | <math>\int dy / \sqrt{(y^2 - a^2)} = \int sec\ t\ dt = \log \left\vert sec\ t + tan\ t \right\vert + C_1</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = log |y + √ (y<sup>2</sup> – a<sup>2</sup>)| + C
| | <math>t</math> का मान पुनः प्रतिस्थापित करने पर, |
|
| |
|
| Substitute y = a sec t
| | <math>\int dy / \sqrt{(y^2 -a^2)} = \log \left\vert (y/a) + \sqrt{[(y^2 -a^2) / a^2]} \right\vert + C_1</math> |
|
| |
|
| So, dy = a sec t tan t dt.
| | इसका समाधान करते हुए, |
|
| |
|
| Therefore,
| | <math>= \log \left\vert y + \sqrt{(y^2 - a^2)} \right\vert - \log \left\vert a \right\vert + C_1</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = ∫ a sec t tan t dt / √ (a<sup>2</sup> sec<sup>2</sup> t – a<sup>2</sup>)
| | अत:, |
|
| |
|
| Solving,
| | <math>= \log \left\vert y + \sqrt{(y^2-a^2)} \right\vert + C</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = ∫ sec t dt = log |sec t + tan t| + C<sub>1</sub>
| | जहाँ, <math>C = C_1 - \log \left\vert a \right\vert</math> |
|
| |
|
| Substituting the value of t again,
| | === फलन 5 का समाकलन === |
| | <math>\int dy / \sqrt{ (a^2- y^2)} = sin^{-1} (y/a) + C</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = log |(y/a) + √ [(y<sup>2</sup> – a<sup>2</sup>) / a<sup>2</sup>]| + C<sub>1</sub>
| | प्रतिस्थापन करने पर <math>y = a \ sin \ t</math> |
|
| |
|
| Solving,
| | <math>dy = a \ cos \ t\ dt</math> |
|
| |
|
| = log |y + √(y<sup>2</sup> – a<sup>2</sup>)| – log |a| + C<sub>1</sub>
| | इसलिए, |
|
| |
|
| Hence,
| | <math>\int dy / \sqrt{(a^2 -y^2)} = \int a\ cos\ t \ dt / {\sqrt{(a^2 -a^2 sin^2 t)}}</math> |
|
| |
|
| = log |y + √(y<sup>2</sup> – a<sup>2</sup>)| + C
| | इसका समाधान करते हुए, |
|
| |
|
| where, C = C<sub>1</sub> – log |a|
| | <math>\int dy / \sqrt{(a^2 - y^2)} = \int t\ dt = t + C</math> |
|
| |
|
| # Integral of Function 5
| | <math>t</math> का मान पुनः प्रतिस्थापित करें, |
|
| |
|
| ∫ dy / √ (a<sup>2</sup> – y<sup>2</sup>) = sin<sup>–1</sup> (y/a) + C
| | <math>\int dy / \sqrt{(a^2 -y^2)} = sin^{-1} (y/a) + C</math> |
|
| |
|
| Substitute y = a sin t
| | === फलन 6 का समाकलन === |
| | <math>\int dy / \sqrt{(y^2 + a^2)} = \log \left\vert y + \sqrt{(y^2 + a^2)} \right\vert + C</math> |
|
| |
|
| dy = a cos t dt.
| | प्रतिस्थापन करने पर <math>y = a \ tan\ t,</math> |
|
| |
|
| Therefore,
| | <math>dy = a sec^2\ t\ dt</math> |
|
| |
|
| ∫ dy / √ (a<sup>2</sup> – y<sup>2</sup>) = ∫ a cos t dt / √ (a<sup>2</sup> – a<sup>2</sup> sin<sup>2</sup> t)
| | इसलिए, |
|
| |
|
| Solving,
| | <math>\int dy / \sqrt{(y^2 + a^2)} = \int a sec^2 t dt / \sqrt{(a^2 tan^2t + a^2)}</math> |
|
| |
|
| ∫ dy / √ (a<sup>2</sup> – y<sup>2</sup>) = ∫ t dt = t + C
| | इसका समाधान करते हुए, |
|
| |
|
| Substituting the value of t,
| | <math>\int dy / \sqrt{(y^2 - a^2)} = \int sec \ t \ dt = \log \left\vert sec\ t + tan\ t \right\vert + C_1</math> |
|
| |
|
| ∫ dy / √ (a<sup>2</sup> – y<sup>2</sup>) = sin<sup>–1</sup> (y/a) + C
| | <math>t</math> का मान पुनः प्रतिस्थापित करें, |
|
| |
|
| # Integral of Function 6
| | <math>\int dy / \sqrt{(y^2 - a^2)} = \log \left\vert (y/a) + \sqrt{[(y^2 + a^2) / a^2]} \right\vert + C_1</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> + a<sup>2</sup>) = log |y + √ (y<sup>2</sup> + a<sup>2</sup>)| + C
| | इसका समाधान करते हुए, |
|
| |
|
| Substitute y = a tan t,
| | <math>= \log \left\vert y + \sqrt{(y2 + a2)} \right\vert-\log\left\vert a \right\vert + C_1</math> |
|
| |
|
| dy = a sec<sup>2</sup> t dt
| | अत:, |
|
| |
|
| Therefore,
| | <math>= \log \left\vert y + \sqrt{(y^2 + a^2)} \right\vert + C</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> + a<sup>2</sup>) = ∫ a sec<sup>2</sup> t dt / √ (a<sup>2</sup> tan<sup>2</sup> t + a<sup>2</sup>)
| | जहाँ, <math>C = C_1 - \log \left\vert a \right\vert</math> |
|
| |
|
| Solving,
| | === फलन 7 का समाकलन === |
| | <math>\int dy / (ay^2 + by + c)</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = ∫ sec t dt = log |sec t + tan t| + C<sub>1</sub>
| | आप इसे इस प्रकार लिख सकते हैं |
|
| |
|
| Re-substituting the value of t,
| | <math>ay^2 + by + c = a [y^2 + (b/a)y + (c/a)]</math> |
|
| |
|
| ∫ dy / √ (y<sup>2</sup> – a<sup>2</sup>) = log |(y/a) + √ [(y<sup>2</sup> + a<sup>2</sup>) / a<sup>2</sup>]| + C<sub>1</sub>
| | इसका समाधान करते हुए, |
|
| |
|
| Solving,
| | <math>a [(y + b/2a)^2 + (c/a- b^2/4a^2)]</math> |
|
| |
|
| = log |y + √(y<sup>2</sup> + a<sup>2</sup>)| – log |a| + C<sub>1</sub>
| | प्रतिस्थापित करें <math>(y + b/2a) = t</math> और आपको <math>dy = dt</math> प्राप्त होगा । |
|
| |
|
| Hence,
| | प्रतिस्थापन <math>(c/a - b^2/4a^2) = \pm k^2</math>। |
|
| |
|
| = log |y + √(y<sup>2</sup> + a<sup>2</sup>)| + C
| | इसलिए, |
|
| |
|
| where, C = C<sub>1</sub> – log |a|
| | <math>ay^2 + by + c = a (t^2 \pm k^2)</math> |
|
| |
|
| # Integral of Function 7
| | जहाँ + या – चिह्न समीकरण <math>(c/a - b^2/4a^2)</math> के चिह्न पर निर्भर करते हैं. |
|
| |
|
| ∫ dy / (ay<sup>2</sup> + by + c)
| | इसलिए, |
|
| |
|
| You can write this as
| | <math>\int dy / (ay^2 + by + c) = 1/a \int dt / (t^2 \pm k^2)</math> |
|
| |
|
| ay<sup>2</sup> + by + c = a [y<sup>2</sup> + (b/a)y + (c/a)]
| | आप ऊपर दिखाए गए siy एकीकरण सूत्रों में से एक या अधिक का उपयोग करके इस समीकरण का मूल्यांकन कर सकते हैं। याद रखें कि आप इसी तरह से समीकरण <math>\int dy / \sqrt{(ay^2 + by + c)}</math> को भी हल कर सकते हैं। |
| | |
| Solving,
| |
| | |
| a [(y + b/2a)<sup>2</sup> + (c/a – b<sup>2</sup>/4a<sup>2</sup>)]
| |
| | |
| Substitute (y + b/2a) = t and you would get dy = dt.
| |
| | |
| Substitute (c/a – b<sup>2</sup>/4a<sup>2</sup>) = ±k<sup>2</sup>.
| |
| | |
| Therefore,
| |
| | |
| ay<sup>2</sup> + by + c = a (t<sup>2</sup> ± k<sup>2</sup>)
| |
| | |
| where the signs + or – depend on the sign of the equation (c/a – b<sup>2</sup>/4a<sup>2</sup>).
| |
| | |
| Therefore,
| |
| | |
| ∫ dy / (ay<sup>2</sup> + by + c) = 1/a ∫ dt / (t<sup>2</sup> ± k<sup>2</sup>)
| |
| | |
| You can evaluate this equation by using one or more of the above siy integration formulas shown. Remember that you can also solve for the equation ∫ dy / √ (ay<sup>2</sup> + by + c) in a similar manner.
| |
| | |
| # Integral of Function 8
| |
|
| |
|
| | === फलन 8 का समाकलन === |
| ∫ [(py + q) / (ay<sup>2</sup> + by + c)] dy, | | ∫ [(py + q) / (ay<sup>2</sup> + by + c)] dy, |
|
| |
|
| where p, q, a, b, c are known to be constants.
| | जहाँ <math>p, q, a, b, c</math> स्थिरांक माने जाते हैं। |
|
| |
|
| To solve this, you must find the constants A and B such that,
| | इसे हल करने के लिए, आपको स्थिरांक <math>A</math> और <math>B</math> ज्ञात करने होंगे, जैसे कि, |
|
| |
|
| (py + q) = A d/dy (ay<sup>2</sup> + by + c) + B, which is equal to = A (2ay + b) + B | | <math>(py + q) = A d/dy (ay^2 + by + c) + B,</math> जो <math>= A (2ay + b) + B</math> बराबर है |
|
| |
|
| To determine ‘A’ and ‘B’, first, equate from both the sides of the coefficients of y and the constant terms. ‘A’ and ‘B’ can then be obtained and therefore, the integral is reduced to any one of the known forms.
| | ‘<math>A</math>’ और ‘<math>B</math>’ निर्धारित करने के लिए, सबसे पहले, y के गुणांकों और स्थिर पदों के दोनों ओर से समान करें। तब ‘<math>A</math>’ और ‘<math>B</math>’ प्राप्त किए जा सकते हैं और इसलिए, समाकल को ज्ञात रूपों में से किसी एक में घटाया जा सकता है। |
|
| |
|
| === '''Solved Example''' === | | == उदाहरण == |
| Find the integral of (y + 3) / √ (5 – 4y + y<sup>2</sup>) with respect to y.
| | <math>y</math> के सापेक्ष <math>(y + 3) / \sqrt{ (5 - 4y + y^2)}</math> का समाकल ज्ञात कीजिए। |
|
| |
|
| Solution
| | समाधान |
|
| |
|
| You can express
| | आप अभिव्यक्त कर सकते हैं |
|
| |
|
| y + 3 = A d/dy (5 – 4y + y<sup>2</sup>) + B = A (– 4 – 2y) + B | | <math>y + 3 = A d/dy (5 - 4y + y^2) + B = A (- 4 - 2y) + B</math> |
|
| |
|
| Equating the coefficients, you get
| | गुणांकों को समान करने पर, आपको प्राप्त होता है |
|
| |
|
| A = – ½ and B = 1 | | <math>A = -{1 \over 2}</math> and <math>B = 1</math> |
|
| |
|
| Therefore,
| | इसलिए, |
|
| |
|
| ∫ [(y + 3) / √ (5 – 4y + y<sup>2</sup>)] dy = – ½ ∫ [(– 4 – 2y) / √ (5 – 4y + y<sup>2</sup>)] dy + ∫ dy / √ (5 – 4y + y<sup>2</sup>)
| | <math>\int [(y + 3) / \sqrt{(5 -4y + y^2)}] dy = -{1 \over 2} \int [(- 4 - 2y) / \sqrt{(5 - 4y + y^2)]} dy + \int dy / \sqrt{(5 - 4y + y^2)}</math> |
|
| |
|
| = – ½ I<sub>1</sub> + I<sub>2</sub> … (a)
| | <math>= -{1 \over 2} I_1 + I_2... (a)</math> |
|
| |
|
| Solving I<sub>1</sub>
| | इसका समाधान करते हुए, <math>I_1</math> |
|
| |
|
| Substitute (5 – 4y + y<sup>2</sup>) = t,
| | प्रतिस्थापन <math>(5 -4y + y^2) = t,</math> |
|
| |
|
| (– 4 – 2y) dy = dt | | <math>(- 4 -2y) dy = dt</math> |
|
| |
|
| Therefore,
| | इसलिए, |
|
| |
|
| I<sub>1</sub> = ∫ [(– 4 – 2y) / √ (5 – 4y + y<sup>2</sup>)] dy = ∫ dt / √ t = 2 √ t + C<sub>1</sub>
| | <math>I_1 = \int [(- 4- 2y) / \sqrt{(5 - 4y + y^2)}] dy = \int dt / \sqrt{t} = 2 \sqrt{t} + C_1</math> |
|
| |
|
| = 2 √ (5 – 4y + y<sup>2</sup>) + C<sub>1</sub> … (b) | | <math>= 2 \sqrt{(5 - 4y + y^2)} + C1...(b)</math> |
|
| |
|
| Solving I<sub>2</sub>
| | इसका समाधान करते हुए, <math>I_2</math> |
|
| |
|
| I<sub>2</sub> = ∫ dy / √ (5 – 4y + y<sup>2</sup>) =
| | <math>I_2 = \int dy / \sqrt{ (5 - 4y + y^2)} =</math> |
|
| |
|
| ∫ dy / √ [9 – (y + 2)<sup>2</sup>]
| | <math>\int dy / \sqrt{[9 - (y + 2)^2}]</math> |
|
| |
|
| Substitute (y + 2) = t,
| | प्रतिस्थापन करते हुए <math>(y + 2) = t,</math> |
|
| |
|
| dy = dt | | <math>dy = dt</math> |
|
| |
|
| Therefore,
| | इसलिए, |
|
| |
|
| I<sub>2</sub> = ∫ dt / √ (3<sup>2</sup> – t<sup>2</sup>) = sin<sup>–1</sup> (t/3) + C<sub>2</sub>
| | <math>I_2 = \int dt / \sqrt{ (3^2 - t^2)} = sin^{-1} (t/3) + C_2</math> |
|
| |
|
| Solving,
| | इसका समाधान करते हुए, |
|
| |
|
| = sin<sup>–1</sup> + C<sub>2</sub> … (c) | | <math>= sin^{-1}(y+2)/3 + C_2... (c)</math> |
|
| |
|
| Substitute (b) and (c) in (a),
| | <math>(a)</math> के स्थान पर <math>(b)</math> और <math>(c)</math> प्रतिस्थापन करने पर , |
|
| |
|
| ∫ [(y + 3) / √ (5 – 4y + y<sup>2</sup>)] dy = – ½ I<sub>1</sub> + I<sub>2</sub>
| | <math>\int [(y + 3) / \sqrt{(5 - 4y + y^2)}] dy = -{1 \over 2} I_1 + I_2</math> |
|
| |
|
| = – √ (5 – 4y + y<sup>2</sup>) + sin<sup>–1</sup> + C | | <math>= -\sqrt{(5 -4y + y^2)} + sin^{-1} + C</math> |
|
| |
|
| where C = C<sub>2</sub> = C<sub>1</sub>/2.
| | जहाँ <math>C = C_2 = C_1/2</math> |
| [[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | | [[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] |
समाकलन एक विधि है, जो बड़े पैमाने पर फलनों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशिष्ट फलनों के समाकलन पर चर्चा करें जो साधारणतः गणना के लिए उपयोग किए जाते हैं। इन समाकलन के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फलन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ।
कई महत्वपूर्ण समाकलन सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशिष्ट फलनों के समाकलनों पर एक दृष्टि डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है।
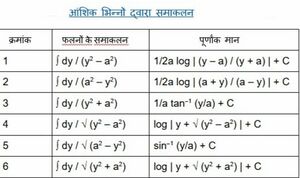
कुछ विशिष्ट फलनों के समाकलन
समाकलन फलनों का प्रमाण
अब जब आप इन समाकलन फलनों और उनके मूल्यों के बारे में जानते हैं, तो आइए इनमें से प्रत्येक फलन के प्रमाण पर एक दृष्टि डालें।
फलन 1 का समाकलन

जैसा कि आप जानते हैं,

इसका समाधान करते हुए,

इसे और कम करते हुए,

अतः, 
इसका समाधान करते हुए,

अत:,

फलन 2 का समाकलन

जैसा कि आप जानते हैं,

इसका समाधान करते हुए,

अत:,

इसलिए, 
जब आप हल करते हैं,

अत:,

फलन 3 का समाकलन

 रखने पर, आपको
रखने पर, आपको  प्राप्त होगा।
प्राप्त होगा।
इसलिए,
![{\displaystyle \int dy/(y^{2}+a^{2})=\int [(a\ sec^{2}\ t\ dt)/(a^{2}\ tan^{2}\ t+a^{2})]}](/index.php?title=Special:MathShowImage&hash=dbcdb397a8a6148b4f72072e73d4b7c3&mode=mathml)
इसका समाधान करते हुए,

 का मान पुनः प्रतिस्थापित करें,
का मान पुनः प्रतिस्थापित करें,

फलन 4 का समाकलन

प्रतिस्थापित 
इसलिए, 
इसलिए,

इसका समाधान करते हुए,

 का मान पुनः प्रतिस्थापित करने पर,
का मान पुनः प्रतिस्थापित करने पर,
![{\displaystyle \int dy/{\sqrt {(y^{2}-a^{2})}}=\log \left\vert (y/a)+{\sqrt {[(y^{2}-a^{2})/a^{2}]}}\right\vert +C_{1}}](/index.php?title=Special:MathShowImage&hash=9b949d56bc26db262a065b175e545d9a&mode=mathml)
इसका समाधान करते हुए,

अत:,

जहाँ, 
फलन 5 का समाकलन

प्रतिस्थापन करने पर 

इसलिए,

इसका समाधान करते हुए,

 का मान पुनः प्रतिस्थापित करें,
का मान पुनः प्रतिस्थापित करें,

फलन 6 का समाकलन

प्रतिस्थापन करने पर 

इसलिए,

इसका समाधान करते हुए,

 का मान पुनः प्रतिस्थापित करें,
का मान पुनः प्रतिस्थापित करें,
![{\displaystyle \int dy/{\sqrt {(y^{2}-a^{2})}}=\log \left\vert (y/a)+{\sqrt {[(y^{2}+a^{2})/a^{2}]}}\right\vert +C_{1}}](/index.php?title=Special:MathShowImage&hash=5dba9b695a20ad5b846615de2cf1affb&mode=mathml)
इसका समाधान करते हुए,

अत:,

जहाँ, 
फलन 7 का समाकलन

आप इसे इस प्रकार लिख सकते हैं
![{\displaystyle ay^{2}+by+c=a[y^{2}+(b/a)y+(c/a)]}](/index.php?title=Special:MathShowImage&hash=791a7dd30a9bfa01a961c736cb79059f&mode=mathml)
इसका समाधान करते हुए,
![{\displaystyle a[(y+b/2a)^{2}+(c/a-b^{2}/4a^{2})]}](/index.php?title=Special:MathShowImage&hash=00accfeea6bc5c84004a9c4e31938d9a&mode=mathml)
प्रतिस्थापित करें  और आपको
और आपको  प्राप्त होगा ।
प्राप्त होगा ।
प्रतिस्थापन  ।
।
इसलिए,

जहाँ + या – चिह्न समीकरण  के चिह्न पर निर्भर करते हैं.
के चिह्न पर निर्भर करते हैं.
इसलिए,

आप ऊपर दिखाए गए siy एकीकरण सूत्रों में से एक या अधिक का उपयोग करके इस समीकरण का मूल्यांकन कर सकते हैं। याद रखें कि आप इसी तरह से समीकरण  को भी हल कर सकते हैं।
को भी हल कर सकते हैं।
फलन 8 का समाकलन
∫ [(py + q) / (ay2 + by + c)] dy,
जहाँ  स्थिरांक माने जाते हैं।
स्थिरांक माने जाते हैं।
इसे हल करने के लिए, आपको स्थिरांक  और
और  ज्ञात करने होंगे, जैसे कि,
ज्ञात करने होंगे, जैसे कि,
 जो
जो  बराबर है
बराबर है
‘ ’ और ‘
’ और ‘ ’ निर्धारित करने के लिए, सबसे पहले, y के गुणांकों और स्थिर पदों के दोनों ओर से समान करें। तब ‘
’ निर्धारित करने के लिए, सबसे पहले, y के गुणांकों और स्थिर पदों के दोनों ओर से समान करें। तब ‘ ’ और ‘
’ और ‘ ’ प्राप्त किए जा सकते हैं और इसलिए, समाकल को ज्ञात रूपों में से किसी एक में घटाया जा सकता है।
’ प्राप्त किए जा सकते हैं और इसलिए, समाकल को ज्ञात रूपों में से किसी एक में घटाया जा सकता है।
उदाहरण
 के सापेक्ष
के सापेक्ष  का समाकल ज्ञात कीजिए।
का समाकल ज्ञात कीजिए।
समाधान
आप अभिव्यक्त कर सकते हैं

गुणांकों को समान करने पर, आपको प्राप्त होता है
 and
and 
इसलिए,
![{\displaystyle \int [(y+3)/{\sqrt {(5-4y+y^{2})}}]dy=-{1 \over 2}\int [(-4-2y)/{\sqrt {(5-4y+y^{2})]}}dy+\int dy/{\sqrt {(5-4y+y^{2})}}}](/index.php?title=Special:MathShowImage&hash=9488b93da792888035bae652649ca633&mode=mathml)

इसका समाधान करते हुए, 
प्रतिस्थापन 

इसलिए,
![{\displaystyle I_{1}=\int [(-4-2y)/{\sqrt {(5-4y+y^{2})}}]dy=\int dt/{\sqrt {t}}=2{\sqrt {t}}+C_{1}}](/index.php?title=Special:MathShowImage&hash=ce1f5cdb459b030055e1ccc7e33bf416&mode=mathml)

इसका समाधान करते हुए, 

![{\displaystyle \int dy/{\sqrt {[9-(y+2)^{2}}}]}](/index.php?title=Special:MathShowImage&hash=4e05e37b0e67f6f084a0504dfe353819&mode=mathml)
प्रतिस्थापन करते हुए 

इसलिए,

इसका समाधान करते हुए,

 के स्थान पर
के स्थान पर  और
और  प्रतिस्थापन करने पर ,
प्रतिस्थापन करने पर ,
![{\displaystyle \int [(y+3)/{\sqrt {(5-4y+y^{2})}}]dy=-{1 \over 2}I_{1}+I_{2}}](/index.php?title=Special:MathShowImage&hash=5c417ed376a39b1c48dec4afacc7112e&mode=mathml)

जहाँ 
