साधारण वक्रों के अंतर्गत क्षेत्रफल: Difference between revisions
(added content) |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
वक्र के | वक्र के अंतर्गत क्षेत्रफल की गणना विभिन्न तरीकों से की जाती है, जिनमें से क्षेत्र ज्ञात करने की प्रतिअवकलज विधि सबसे लोकप्रिय है। वक्र के नीचे का क्षेत्र वक्र के समीकरण, वक्र की सीमाओं और वक्र को घेरने वाली धुरी को जानकर पाया जा सकता है। साधारणतः, हमारे पास नियमित आकृतियों जैसे वर्ग, आयत, [[चतुर्भुज]], बहुभुज, [[वृत्त]] के क्षेत्रों को ज्ञात करने के लिए सूत्र होते हैं, लेकिन वक्र के नीचे का क्षेत्र ज्ञात करने के लिए कोई निश्चित सूत्र नहीं है। समाकलन की प्रक्रिया समीकरण को हल करने और आवश्यक क्षेत्र ज्ञात करने में सहायता करती है। | ||
अनियमित समतल सतहों के क्षेत्रफल ज्ञात करने के लिए प्रतिअवकलज विधियाँ बहुत सहायक होती हैं। यहाँ हम सीखेंगे कि अक्ष के सापेक्ष वक्र के | अनियमित समतल सतहों के क्षेत्रफल ज्ञात करने के लिए प्रतिअवकलज विधियाँ बहुत सहायक होती हैं। यहाँ हम सीखेंगे कि अक्ष के सापेक्ष वक्र के अंतर्गत क्षेत्रफल कैसे ज्ञात करें। | ||
[[File:वक्र के अंतर्गत क्षेत्रफल.jpg|thumb|वक्र के अंतर्गत क्षेत्रफल]] | |||
वक्र के नीचे का क्षेत्रफल | == वक्र के अंतर्गत क्षेत्रफल ज्ञात करने की विधि == | ||
वक्र के नीचे का क्षेत्रफल तीन सरल चरणों के माध्यम से गणना किया जा सकता है। सबसे पहले, हमें वक्र का समीकरण <math>(y = f(x)),</math> वह सीमा जिसके पार क्षेत्रफल की गणना की जानी है, और क्षेत्रफल को घेरने वाली अक्ष को जानना होगा। दूसरे, हमें वक्र का समाकलन (प्रतिअवकलज) ज्ञात करना होगा। अंत में, हमें [[समाकलन की विधियाँ|समाकलन]] उत्तर पर ऊपरी सीमा और निचली सीमा लागू करने और वक्र के नीचे का क्षेत्रफल प्राप्त करने के लिए अंतर लेने की आवश्यकता है। | |||
क्षेत्रफल <math>=\ _a\int_{}^{b } y\cdot dx</math> | |||
<math>=\ _a\int_{}^{b } f(x) dx</math> | |||
<math>=[g(x)]_a ^b </math> | |||
<math>=g(b)-g(a)</math> | |||
== विभिन्न विधियाँ == | |||
वक्र के नीचे का क्षेत्रफल तीन विधियों का उपयोग करके गणना किया जा सकता है। साथ ही, वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए उपयोग की जाने वाली विधि वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए आवश्यकता और उपलब्ध डेटा इनपुट पर निर्भर करती है। यहाँ हम वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई तीन विधियों पर विचार करेंगे। | वक्र के नीचे का क्षेत्रफल तीन विधियों का उपयोग करके गणना किया जा सकता है। साथ ही, वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए उपयोग की जाने वाली विधि वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए आवश्यकता और उपलब्ध डेटा इनपुट पर निर्भर करती है। यहाँ हम वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई तीन विधियों पर विचार करेंगे। | ||
विधि - I: यहाँ वक्र के नीचे का क्षेत्र सबसे छोटे संभव आयतों में विभाजित किया गया है। इन आयतों के क्षेत्रफल का योग वक्र के नीचे का क्षेत्रफल देता है। वक्र y = f(x) के लिए, इसे चौड़ाई | === विधि - I: === | ||
यहाँ वक्र के नीचे का क्षेत्र सबसे छोटे संभव आयतों में विभाजित किया गया है। इन आयतों के क्षेत्रफल का योग वक्र के नीचे का क्षेत्रफल देता है। वक्र <math>y = f(x),</math> के लिए, इसे चौड़ाई <math>\delta x</math> के कई आयतों में विभाजित किया जाता है। यहाँ हम आयतों की संख्या को अनंत तक सीमित रखते हैं। वक्र के नीचे कुल क्षेत्रफल का सूत्र <math>A = \textstyle \lim_{x \to \infty} \displaystyle \textstyle \sum_{i=1}^n \displaystyle f(x)\cdot \delta x</math> | |||
x | |||
के कई आयतों में विभाजित किया जाता है। यहाँ हम आयतों की संख्या को अनंत तक सीमित रखते हैं। वक्र के नीचे कुल क्षेत्रफल का सूत्र A = | |||
x | |||
i | |||
= | |||
1 | |||
f | |||
( | |||
x | |||
) | |||
=== विधि - II: === | |||
यह विधि भी वक्र के नीचे का क्षेत्र ज्ञात करने के लिए ऊपर बताई गई प्रक्रिया के समान ही प्रक्रिया का उपयोग करती है। यहाँ वक्र के अंतर्गत क्षेत्रफल को कुछ आयतों में विभाजित किया जाता है। इसके अलावा, वक्र के नीचे का क्षेत्र प्राप्त करने के लिए इन आयतों के क्षेत्रों को जोड़ा जाता है। यह विधि वक्र के नीचे का क्षेत्र ज्ञात करने की एक आसान विधि है, लेकिन यह केवल वक्र के अंतर्गत क्षेत्रफल का अनुमानित मान प्रदान करती है। | |||
=== विधि - III: === | |||
यह विधि वक्र के नीचे का क्षेत्र ज्ञात करने के लिए समाकलन प्रक्रिया का उपयोग करती है। इस विधि समाकलन द्वारा वक्र के नीचे का क्षेत्र ज्ञात करने के लिए हमें वक्र के समीकरण, परिसीमा रेखाओं या अक्ष के ज्ञान और परिसीमा सीमित बिंदुओं की आवश्यकता होती है। एक वक्र के लिए जिसका समीकरण <math>y = f(x),</math> है, और जो <math>x</math>-अक्ष से घिरा है और जिसकी सीमा मान क्रमशः <math>a</math> और <math>b</math> है, वक्र के अंतर्गत क्षेत्रफल का सूत्र है <math>A=\ _a\int_{}^{b } f(x)\cdot dx</math> | |||
x | == वक्र के अंतर्गत क्षेत्रफल के लिए सूत्र == | ||
वक्र के क्षेत्र की गणना विभिन्न अक्षों के संबंध में की जा सकती है, जो दिए गए वक्र की सीमा के रूप में है। वक्र के अंतर्गत क्षेत्रफल की गणना <math>x</math>-अक्ष या <math>y</math>-अक्ष के संबंध में की जा सकती है। विशेष मामलों के लिए, वक्र अक्षों के नीचे होता है, और आंशिक रूप से अक्षों के नीचे होता है। इन सभी मामलों के लिए हमारे पास वक्र के नीचे का क्षेत्र ज्ञात करने के लिए व्युत्पन्न सूत्र है। | |||
[[File:X-अक्ष के सापेक्ष क्षेत्रफल.jpg|thumb|245x245px|X-अक्ष के सापेक्ष क्षेत्रफल]] | |||
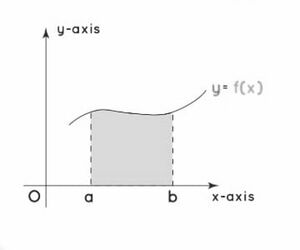
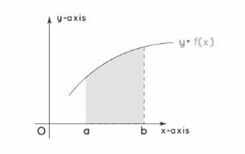
'''<math>x</math>-अक्ष के सापेक्ष क्षेत्रफल''': यहाँ हम सबसे पहले वक्र <math>y = f(x),</math> और <math>x</math>-अक्ष द्वारा परिबद्ध क्षेत्रफल को देखेंगे। नीचे दिए गए चित्र वक्र और <math>x</math>-अक्ष द्वारा परिबद्ध क्षेत्रफल को दर्शाते हैं। <math>x</math>-अक्ष के सापेक्ष वक्र के लिए परिबद्ध मान क्रमशः <math>a</math> और <math>b</math> हैं। <math>x</math>-अक्ष के सापेक्ष वक्र के अंतर्गत क्षेत्रफल ज्ञात करने का सूत्र है <math>A=\ _a\int_{}^{b } f(x)\cdot dx</math> | |||
[[File:Y-अक्ष के सापेक्ष क्षेत्रफल.jpg|thumb|Y-अक्ष के सापेक्ष क्षेत्रफल]] | |||
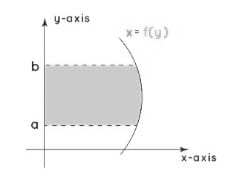
वक्र के नीचे के क्षेत्र | <math>y</math>'''-अक्ष के सापेक्ष क्षेत्रफल''': वक्र x = f(y), <math>y</math>-अक्ष द्वारा परिबद्ध वक्र का क्षेत्रफल, रेखाओं y = a और y = b के पार, नीचे दिए गए व्यंजक द्वारा दिया गया है। इसके अलावा, वक्र और <math>y</math>-अक्ष के बीच के क्षेत्र को नीचे दिए गए ग्राफ से समझा जा सकता है। | ||
<math>A=\ _a\int_{}^{b } x \cdot dy = \ _a\int_{}^{b } f(y)\cdot dy</math> | |||
[[File:अक्ष के अंतर्गत क्षेत्रफल.jpg|thumb|247x247px|अक्ष के अंतर्गत क्षेत्रफल]] | |||
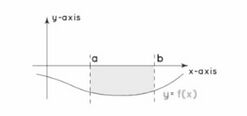
'''अक्ष के अंतर्गत क्षेत्रफल :''' अक्ष के नीचे वक्र का क्षेत्र ऋणात्मक मान है और इसलिए क्षेत्र का मापांक लिया जाता है। <math>x</math>-अक्ष के नीचे और <math>x</math>-अक्ष से घिरे वक्र <math>y = f(x),</math> का क्षेत्र <math>a</math> और <math>b</math> की सीमाएँ लेकर प्राप्त किया जाता है। वक्र और <math>x</math>-अक्ष के ऊपर के क्षेत्र का सूत्र इस प्रकार है। <math>A=\left\vert \ _a\int_{}^{b } f(x)\cdot dx \right\vert</math> | |||
[[File:अक्ष के ऊपर और नीचे का क्षेत्र.jpg|thumb|250x250px|अक्ष के ऊपर और नीचे का क्षेत्र]] | |||
'''अक्ष के ऊपर और नीचे का क्षेत्र:''' वक्र का वह क्षेत्र जो आंशिक रूप से अक्ष के नीचे और आंशिक रूप से अक्ष के ऊपर है, उसे दो क्षेत्रों में विभाजित किया जाता है और अलग-अलग गणना की जाती है। अक्ष के नीचे का क्षेत्र ऋणात्मक है, और इसलिए क्षेत्र का मापांक लिया जाता है। इसलिए कुल क्षेत्रफल दो क्षेत्रों के योग के बराबर है | |||
<math>(A=|A1|+A2)</math> | |||
<math>A=\left\vert \ _a\int_{}^{b } f(x)\cdot dx \right\vert + \ _b\int_{}^{c } f(x)\cdot dx </math> | |||
[[File:वक्र के अंतर्गत क्षेत्रफल - वृत्त.jpg|thumb|256x256px|वक्र के अंतर्गत क्षेत्रफल - वृत्त]] | |||
== वक्र के अंतर्गत क्षेत्रफल - वृत्त == | |||
वृत्त के क्षेत्रफल की गणना पहले चतुर्थांश में वृत्त के भाग के क्षेत्रफल की गणना करके की जाती है। यहाँ वृत्त <math>x^2 + y^2 = a^2</math> के समीकरण को <math>y = \sqrt{(a^2 - x^2)}</math> के रूप में वक्र के समीकरण में बदल दिया जाता है। वक्र के इस समीकरण का उपयोग <math>x</math>-अक्ष के सापेक्ष क्षेत्रफल और <math>0</math> से <math>a</math> तक की सीमाएँ ज्ञात करने के लिए किया जाता है। | |||
वक्र के | |||
वृत्त के क्षेत्रफल की गणना पहले चतुर्थांश में वृत्त के भाग के क्षेत्रफल की गणना करके की जाती है। यहाँ वृत्त | |||
| Line 100: | Line 65: | ||
वृत्त का क्षेत्रफल वृत्त के चतुर्थांश के क्षेत्रफल का चार गुना है। चतुर्थांश के क्षेत्रफल की गणना प्रथम चतुर्थांश में सीमाओं के पार वक्र के समीकरण को एकीकृत करके की जाती है। | वृत्त का क्षेत्रफल वृत्त के चतुर्थांश के क्षेत्रफल का चार गुना है। चतुर्थांश के क्षेत्रफल की गणना प्रथम चतुर्थांश में सीमाओं के पार वक्र के समीकरण को एकीकृत करके की जाती है। | ||
A | <math>A= 4 \int_{0}^{a } y\cdot dx</math> | ||
= 4 | |||
<math>= 4 \int_{0}^{a } \sqrt{a^2-x^2}\cdot dx</math> | |||
= | <math>= 4[ \frac{x}{2} \sqrt{a^2-x^2} +\frac{a^2}{2}sin^{-1}\frac{x}{a}]_{0}^{a} </math> | ||
= | <math>= 4[((\frac{a}{2})\times 0 +(\frac{a^2}{2})sin^{-1}1)-0] </math> | ||
= | <math>= 4(a^2/2)(\pi/2) </math> | ||
= | <math>= \pi a^2 </math> sq.unit | ||
अतः वृत्त का क्षेत्रफल <math>\pi a^2 </math> वर्ग इकाई है। | |||
[[File:वक्र के अंतर्गत क्षेत्रफल - परवलय.jpg|thumb|275x275px|वक्र के अंतर्गत क्षेत्रफल - परवलय]] | |||
== वक्र के अंतर्गत क्षेत्रफल - परवलय == | |||
एक परवलय में एक अक्ष होता है जो परवलय को दो सममित भागों में विभाजित करता है। यहाँ हम एक परवलय लेते हैं जो x-अक्ष के साथ सममित है और इसका समीकरण <math>y^2 = 4ax</math> है। इसे <math>y = \sqrt{(4ax)}</math> के रूप में बदला जा सकता है। हम सबसे पहले <math>x</math>-अक्ष के संबंध में और <math>0</math> से <math>a</math> तक की सीमाओं के साथ पहले चतुर्थांश में परवलय का क्षेत्र ज्ञात करते हैं। यहाँ हम समीकरण को सीमा के भीतर एकीकृत करते हैं और इसे दोगुना करते हैं, ताकि पूरे परवलय का क्षेत्र प्राप्त हो सके। परवलय के क्षेत्र के लिए व्युत्पन्न इस प्रकार है। | |||
a | <math>A= 2 \int_{0}^{a } \sqrt{(4ax)}\cdot dx</math> | ||
<math>A= 4\sqrt{a} \int_{0}^{a } \sqrt{x}\cdot dx</math> | |||
3 | <math>A= 4\sqrt{a}[\frac{2}{3}\cdot x^{\frac{3}{2}}] _{0}^{a } </math> | ||
<math>A= 4\sqrt{a}((\frac{2}{3}\cdot a^{\frac{3}{2}}) _{0}^{a }-0) </math> | |||
<math>= \frac{8a^2}{3}</math> | |||
इसलिए परवलय द्वारा परिबद्ध वक्र के नीचे का क्षेत्रफल <math>\frac{8a^2}{3}</math> वर्ग इकाई है। | |||
[[Category:समकलनों के अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:समकलनों के अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-12]] | ||
Latest revision as of 08:26, 8 December 2024
वक्र के अंतर्गत क्षेत्रफल की गणना विभिन्न तरीकों से की जाती है, जिनमें से क्षेत्र ज्ञात करने की प्रतिअवकलज विधि सबसे लोकप्रिय है। वक्र के नीचे का क्षेत्र वक्र के समीकरण, वक्र की सीमाओं और वक्र को घेरने वाली धुरी को जानकर पाया जा सकता है। साधारणतः, हमारे पास नियमित आकृतियों जैसे वर्ग, आयत, चतुर्भुज, बहुभुज, वृत्त के क्षेत्रों को ज्ञात करने के लिए सूत्र होते हैं, लेकिन वक्र के नीचे का क्षेत्र ज्ञात करने के लिए कोई निश्चित सूत्र नहीं है। समाकलन की प्रक्रिया समीकरण को हल करने और आवश्यक क्षेत्र ज्ञात करने में सहायता करती है।
अनियमित समतल सतहों के क्षेत्रफल ज्ञात करने के लिए प्रतिअवकलज विधियाँ बहुत सहायक होती हैं। यहाँ हम सीखेंगे कि अक्ष के सापेक्ष वक्र के अंतर्गत क्षेत्रफल कैसे ज्ञात करें।
वक्र के अंतर्गत क्षेत्रफल ज्ञात करने की विधि
वक्र के नीचे का क्षेत्रफल तीन सरल चरणों के माध्यम से गणना किया जा सकता है। सबसे पहले, हमें वक्र का समीकरण वह सीमा जिसके पार क्षेत्रफल की गणना की जानी है, और क्षेत्रफल को घेरने वाली अक्ष को जानना होगा। दूसरे, हमें वक्र का समाकलन (प्रतिअवकलज) ज्ञात करना होगा। अंत में, हमें समाकलन उत्तर पर ऊपरी सीमा और निचली सीमा लागू करने और वक्र के नीचे का क्षेत्रफल प्राप्त करने के लिए अंतर लेने की आवश्यकता है।
क्षेत्रफल
विभिन्न विधियाँ
वक्र के नीचे का क्षेत्रफल तीन विधियों का उपयोग करके गणना किया जा सकता है। साथ ही, वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए उपयोग की जाने वाली विधि वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए आवश्यकता और उपलब्ध डेटा इनपुट पर निर्भर करती है। यहाँ हम वक्र के नीचे का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई तीन विधियों पर विचार करेंगे।
विधि - I:
यहाँ वक्र के नीचे का क्षेत्र सबसे छोटे संभव आयतों में विभाजित किया गया है। इन आयतों के क्षेत्रफल का योग वक्र के नीचे का क्षेत्रफल देता है। वक्र के लिए, इसे चौड़ाई के कई आयतों में विभाजित किया जाता है। यहाँ हम आयतों की संख्या को अनंत तक सीमित रखते हैं। वक्र के नीचे कुल क्षेत्रफल का सूत्र
विधि - II:
यह विधि भी वक्र के नीचे का क्षेत्र ज्ञात करने के लिए ऊपर बताई गई प्रक्रिया के समान ही प्रक्रिया का उपयोग करती है। यहाँ वक्र के अंतर्गत क्षेत्रफल को कुछ आयतों में विभाजित किया जाता है। इसके अलावा, वक्र के नीचे का क्षेत्र प्राप्त करने के लिए इन आयतों के क्षेत्रों को जोड़ा जाता है। यह विधि वक्र के नीचे का क्षेत्र ज्ञात करने की एक आसान विधि है, लेकिन यह केवल वक्र के अंतर्गत क्षेत्रफल का अनुमानित मान प्रदान करती है।
विधि - III:
यह विधि वक्र के नीचे का क्षेत्र ज्ञात करने के लिए समाकलन प्रक्रिया का उपयोग करती है। इस विधि समाकलन द्वारा वक्र के नीचे का क्षेत्र ज्ञात करने के लिए हमें वक्र के समीकरण, परिसीमा रेखाओं या अक्ष के ज्ञान और परिसीमा सीमित बिंदुओं की आवश्यकता होती है। एक वक्र के लिए जिसका समीकरण है, और जो -अक्ष से घिरा है और जिसकी सीमा मान क्रमशः और है, वक्र के अंतर्गत क्षेत्रफल का सूत्र है
वक्र के अंतर्गत क्षेत्रफल के लिए सूत्र
वक्र के क्षेत्र की गणना विभिन्न अक्षों के संबंध में की जा सकती है, जो दिए गए वक्र की सीमा के रूप में है। वक्र के अंतर्गत क्षेत्रफल की गणना -अक्ष या -अक्ष के संबंध में की जा सकती है। विशेष मामलों के लिए, वक्र अक्षों के नीचे होता है, और आंशिक रूप से अक्षों के नीचे होता है। इन सभी मामलों के लिए हमारे पास वक्र के नीचे का क्षेत्र ज्ञात करने के लिए व्युत्पन्न सूत्र है।
-अक्ष के सापेक्ष क्षेत्रफल: यहाँ हम सबसे पहले वक्र और -अक्ष द्वारा परिबद्ध क्षेत्रफल को देखेंगे। नीचे दिए गए चित्र वक्र और -अक्ष द्वारा परिबद्ध क्षेत्रफल को दर्शाते हैं। -अक्ष के सापेक्ष वक्र के लिए परिबद्ध मान क्रमशः और हैं। -अक्ष के सापेक्ष वक्र के अंतर्गत क्षेत्रफल ज्ञात करने का सूत्र है
-अक्ष के सापेक्ष क्षेत्रफल: वक्र x = f(y), -अक्ष द्वारा परिबद्ध वक्र का क्षेत्रफल, रेखाओं y = a और y = b के पार, नीचे दिए गए व्यंजक द्वारा दिया गया है। इसके अलावा, वक्र और -अक्ष के बीच के क्षेत्र को नीचे दिए गए ग्राफ से समझा जा सकता है।
अक्ष के अंतर्गत क्षेत्रफल : अक्ष के नीचे वक्र का क्षेत्र ऋणात्मक मान है और इसलिए क्षेत्र का मापांक लिया जाता है। -अक्ष के नीचे और -अक्ष से घिरे वक्र का क्षेत्र और की सीमाएँ लेकर प्राप्त किया जाता है। वक्र और -अक्ष के ऊपर के क्षेत्र का सूत्र इस प्रकार है।
अक्ष के ऊपर और नीचे का क्षेत्र: वक्र का वह क्षेत्र जो आंशिक रूप से अक्ष के नीचे और आंशिक रूप से अक्ष के ऊपर है, उसे दो क्षेत्रों में विभाजित किया जाता है और अलग-अलग गणना की जाती है। अक्ष के नीचे का क्षेत्र ऋणात्मक है, और इसलिए क्षेत्र का मापांक लिया जाता है। इसलिए कुल क्षेत्रफल दो क्षेत्रों के योग के बराबर है
वक्र के अंतर्गत क्षेत्रफल - वृत्त
वृत्त के क्षेत्रफल की गणना पहले चतुर्थांश में वृत्त के भाग के क्षेत्रफल की गणना करके की जाती है। यहाँ वृत्त के समीकरण को के रूप में वक्र के समीकरण में बदल दिया जाता है। वक्र के इस समीकरण का उपयोग -अक्ष के सापेक्ष क्षेत्रफल और से तक की सीमाएँ ज्ञात करने के लिए किया जाता है।
वृत्त का क्षेत्रफल वृत्त के चतुर्थांश के क्षेत्रफल का चार गुना है। चतुर्थांश के क्षेत्रफल की गणना प्रथम चतुर्थांश में सीमाओं के पार वक्र के समीकरण को एकीकृत करके की जाती है।
sq.unit
अतः वृत्त का क्षेत्रफल वर्ग इकाई है।
वक्र के अंतर्गत क्षेत्रफल - परवलय
एक परवलय में एक अक्ष होता है जो परवलय को दो सममित भागों में विभाजित करता है। यहाँ हम एक परवलय लेते हैं जो x-अक्ष के साथ सममित है और इसका समीकरण है। इसे के रूप में बदला जा सकता है। हम सबसे पहले -अक्ष के संबंध में और से तक की सीमाओं के साथ पहले चतुर्थांश में परवलय का क्षेत्र ज्ञात करते हैं। यहाँ हम समीकरण को सीमा के भीतर एकीकृत करते हैं और इसे दोगुना करते हैं, ताकि पूरे परवलय का क्षेत्र प्राप्त हो सके। परवलय के क्षेत्र के लिए व्युत्पन्न इस प्रकार है।
इसलिए परवलय द्वारा परिबद्ध वक्र के नीचे का क्षेत्रफल वर्ग इकाई है।