अवकलाजों का सहजानुभूत बोध: Difference between revisions
(added table) |
(added table) |
||
| Line 14: | Line 14: | ||
उनका उपयोग उन अंतरालों को ज्ञात करने के लिए भी किया जाता है जहाँ फलन बढ़ रहा है/घट रहा है और साथ ही उन अंतरालों को भी जहाँ फलन ऊपर/नीचे अवतल है। | उनका उपयोग उन अंतरालों को ज्ञात करने के लिए भी किया जाता है जहाँ फलन बढ़ रहा है/घट रहा है और साथ ही उन अंतरालों को भी जहाँ फलन ऊपर/नीचे अवतल है। | ||
इस प्रकार, जब भी हम "ढलान/ढाल", "परिवर्तन की दर", "वेग (विस्थापन दिया गया)", "अधिकतम/न्यूनतम" आदि जैसे वाक्यांश देखते हैं तो इसका मतलब है कि अवकलाजों की अवधारणा उपस्थित है। | इस प्रकार, जब भी हम "ढलान/ढाल", "परिवर्तन की दर", "वेग (विस्थापन दिया गया)", "अधिकतम/न्यूनतम" आदि जैसे वाक्यांश देखते हैं तो इसका मतलब है कि अवकलाजों की अवधारणा उपस्थित है। | ||
{| class="wikitable" | {| class="wikitable" | ||
Revision as of 11:50, 23 November 2024
कलन(कैलकुलस) में व्युत्पन्न एक राशि के दूसरी राशि के सापेक्ष परिवर्तन की दर है। इसे के सापेक्ष का अंतर गुणांक भी कहा जाता है। विभेदन किसी फलन का व्युत्पन्न ज्ञात करने की प्रक्रिया है। आइए जानें कि कलन में व्युत्पन्न का वास्तव में क्या अर्थ है और नियमों और उदाहरणों के साथ इसे कैसे ज्ञात करना है।
अवकलाजों की व्याख्या
गणित में फलन के अवकलाज को द्वारा दर्शाया जाता है और इसे संदर्भ के अनुसार इस प्रकार से व्याख्यायित किया जा सकता है:
किसी बिंदु पर फलन का अवकलाज उस बिंदु पर उस वक्र पर खींची गई स्पर्शरेखा का ढलान होता है।
यह फलन पर किसी बिंदु पर परिवर्तन की तात्कालिक दर को भी दर्शाता है।
विस्थापन फलन के व्युत्पन्न को ज्ञात करके किसी कण का वेग ज्ञात किया जाता है।
अवकलाजों का उपयोग फलन को अनुकूलित (अधिकतम/न्यूनतम) करने के लिए किया जाता है।
उनका उपयोग उन अंतरालों को ज्ञात करने के लिए भी किया जाता है जहाँ फलन बढ़ रहा है/घट रहा है और साथ ही उन अंतरालों को भी जहाँ फलन ऊपर/नीचे अवतल है।
इस प्रकार, जब भी हम "ढलान/ढाल", "परिवर्तन की दर", "वेग (विस्थापन दिया गया)", "अधिकतम/न्यूनतम" आदि जैसे वाक्यांश देखते हैं तो इसका मतलब है कि अवकलाजों की अवधारणा उपस्थित है।
| t | s |
|---|---|
| 0 | 0 |
| 1 | 4.9 |
| 1.5 | 11.025 |
| 1.8 | 15.876 |
| 1.9 | 17.689 |
| 1.95 | 18.63225 |
| 2 | 19.6 |
| 2.05 | 20.59225 |
| 2.1 | 21.609 |
| 2.2 | 23.716 |
| 2.5 | 30.625 |
| 3 | 44.1 |
| 4 | 78.4 |
अवकलाजों का सहजानुभूत बोध
भौतिक प्रयोगों ने अनुमोदित किया है कि पिंड एक खड़ी / ऊँची चट्टान से गिरकर सेकंडों में मीटर दूरी तय करता है अर्थात् पिंड द्वारा मीटर में तय की गई दूरी () सेकंडों में मापे गए समय () के एक फलन के रूप में से दी गई है।
संलग्न सारणी-1 में एक खड़ी ऊँची चट्टान से गिराए गए एक पिंड के सेकंडों में विभिन्न समय () पर मीटर में तय की दूरी () दी गई है।
इन आँकड़ों से समय सेकंड पर पिंड का वेग ज्ञात करना ही उद्देश्य है। इस समस्या तक पहुँचने के लिए सेकंड पर समाप्त होने बाले विविध समयांतरालों पर माध्य वेग ज्ञात करना एक ढंग है और आशा करते हैं कि इससे 12 सेकंड पर वेग के बारे में कुछ प्रकाश पड़ेगा।
,और के बीच माध्य वेग और सेकंडों के बीच तय की गई दूरी को () से भाग देने पर प्राप्त होता है। अतः प्रथम सेकंडों में माध्य वेग
और के बीच तय की गई दूरी / समयांतराल ()
मी / से मी /से
इसी प्रकार, और के बीच माध्य वेग का परिकलन करते हैं।
निम्नलिखित सारणी-2, सेकंडों और सेकंडों के बीच मीटर प्रति सेकंड में माध्य वेग () देती है।
इस सारणी से हम अवलोकन करते हैं कि माध्य वेग धीरे-धीरे बढ़ रहा है। जैसे-जैसे पर समाप्त होने वाले समयांतरालोंको लघुत्तर बनाते जाते हैं हम देखते हैं कि पर हम वेग का एक बहुत अच्छा बोध कर पाते हैं। आशा करते हैं कि सेकंड और सेकंड के बीच कुछ अप्रत्याशित घटना न घटे तो हम निष्कर्ष निकालते हैं कि सेकंड पर माध्य वेग मी/से से थोड़ा अधिक है।
इस निष्कर्ष को निम्नलिखित अभिकलनों के समुच्चय से किंचित बल मिलता है । सेकंड से प्रारंभ करते हुए विविध समयांतरालों पर माध्य वेग का परिकलन कीजिए। पूर्व की भाँति सेकंड और सेकंड के बीच माध्य वेग ()
सेकंड और सेकंड के बीच तय की दूरी/
सेकंड में तय की दूरी /
निम्नलिखित सारणी-3, सेकंडों और सेकंड के बीच मीटर प्रति सेकंड में माध्य वेग () देती है:
सारणी 13.3
यहाँ पुनः हम ध्यान देते हैं कि यदि हम , से प्रारंभ करते हुए लघुत्तर समयान्तरालों को लेते जाते हैं तो हमें पर वेग का अधिक अच्छा बोध होता है।
अभिकलनों के प्रथम समुच्चय में हमने पर समाप्त होने वाले बढ़ते समयान्तरालों में माध्य वेग ज्ञात किया है और तब आशा की है कि से किंचित पूर्व कुछ अप्रत्याशित घटना न घटे। अभिकलनों के द्वितीय समुच्चय में पर अंत होने वाले घटते समयांतरालों में माध्य वेग ज्ञात किया है और तब आशा की है कि के किंचित बाद कुछ अप्रत्याशित घटना न घटे । विशुद्ध रूप से भौतिकीय आधार पर माध्य वेग के ये दोनों अनुक्रम एक समान सीमा पर पहुँचने चाहिए हम निश्चित रूप से निष्कर्ष निकालते हैं कि पर पिंड का वेग मी/से और मी/से के बीच है। तकनीकी रूप से हम कह सकते हैं कि पर तात्कालिक वेग मी / से. और मी/से. के बीच है। जैसा कि भली प्रकार ज्ञात है कि वेग दूरी के परिवर्तन की दर है। अतः हमने जो निष्पादित किया, वह निम्नलिखित है। " विविध क्षण पर दूरी में परिवर्तन की दर का अनुमान लगाया है। हम कहते हैं कि दूरी फलन का पर अवकलज और के बीच में है। "
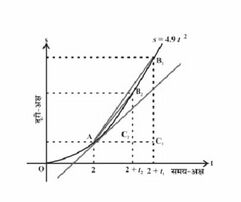
इस सीमा की प्रक्रिया की एक विकल्प विधि चित्र-1 में दर्शाई गई है।
यह बीते समय () और चट्टान के शिखर से पिंड की दूरी () का आलेख है। जैसे-जैसे समयांतरालों के अनुक्रम की सीमा शून्य की ओर अग्रसर होती है वैसे ही माध्य वेगों के अग्रसर होने की वही सीमा होती है जो
के अनुपातों के अनुक्रम की होती है, जहाँ वह दूरी है जो पिंड समयांतरालों में तय करता है, इत्यादि । चित्र- से यह निष्कर्ष निकलना सुनिश्चित है कि यह बाद की अनुक्रम वक्र के बिंदु A पर स्पर्शरेखा के ढाल की ओर अग्रसर होती है। दूसरे शब्दों में, समय पर पिंड का तात्कालिक वेग वक्र के पर स्पर्शी के ढाल के समान है।