फलन का प्रतिलोम: Difference between revisions

Revision as of 07:46, 28 November 2024

व्युत्क्रम फलन को मूल फलन f के संबंध में f-1 द्वारा दर्शाया जाता है और मूल फलन का डोमेन व्युत्क्रम फलन की श्रेणी बन जाता है और दिए गए फलन की श्रेणी व्युत्क्रम फलन का डोमेन बन जाती है। व्युत्क्रम फलन का ग्राफ़ रेखा y = x के संदर्भ में (x, y) को (y, x) से बदलकर प्राप्त किया जाता है।

आइए व्युत्क्रम फ़ंक्शन, व्युत्क्रम फलन को खोजने के चरणों और व्युत्क्रम फलन के ग्राफ़ के बारे में अधिक जानें।

एक फलन मानों को स्वीकार करता है, इन मानों पर विशेष ऑपरेशन करता है और आउटपुट उत्पन्न करता है। व्युत्क्रम फलन परिणामी के साथ सहमत होता है, संचालित होता है और मूल फलन पर वापस पहुँचता है।

परिभाषा

फलन f का व्युत्क्रम f-1 द्वारा दर्शाया जाता है और यह केवल तभी मौजूद होता है जब f एक-एक और आच्छादक फलन दोनों हो। ध्यान दें कि f-1, f का व्युत्क्रम नहीं है। फलन f और आच्छादक फलन f-1 की संरचना x का डोमेन मान देती है।

(f o f-1) (x) = (f-1 o f) (x) = x

फलन 'f' को व्युत्क्रम फलन माना जाने के लिए, y ∈ Y श्रेणी में प्रत्येक तत्व को डोमेन सेट में किसी तत्व x ∈ X से मैप किया गया है, और इस तरह के संबंध को एक-एक संबंध या निषेधाज्ञा संबंध कहा जाता है। साथ ही दिए गए फलन के व्युत्क्रम f-1 का डोमेन y ∈ Y है जो सह-डोमेन सेट में एक अलग तत्व x ∈ X से संबंधित है, और दिए गए फलन 'f' के संदर्भ में इस तरह का संबंध एक आच्छादक फलन या एक प्रक्षेपण फलन है। इस प्रकार व्युत्क्रम फलन एक निषेधात्मक और एक अधिरोपण फलन होने के कारण, एक द्विआवेशन फलन कहलाता है।

आइए एक फलन f पर विचार करें जिसका डोमेन सेट X है और सहडोमेन सेट Y है। फलन f व्युत्क्रमणीय है यदि कोई अन्य फलन g मौजूद है जिसका डोमेन Y है और इसका सहडोमेन X है। इन दो फलन को f(x) = Y, और g(y) = X के रूप में दर्शाया जा सकता है। इस स्थिति के लिए, यदि फलन f(x) व्युत्क्रम है, तो इसका व्युत्क्रम फलन g(x) अद्वितीय है।

यदि दो फलन f(x), और g(x) की संरचना के परिणामस्वरूप एक पहचान फलन f(g(x))= x होता है, तो दोनों फलन एक दूसरे के व्युत्क्रम कहलाते हैं। यदि x पर इनपुट के रूप में फलन के अनुप्रयोग से y का n आउटपुट मिलता है, तो y पर दूसरे फलन g के अनुप्रयोग से x का मान वापस मिलना चाहिए। इसलिए फलन का व्युत्क्रम फलन को उलट देता है। दिए गए फलन का डोमेन व्युत्क्रम फलन की श्रेणी बन जाता है, और दिए गए फलन की श्रेणी व्युत्क्रम फलन का डोमेन बन जाती है।

व्युत्क्रम फलन ज्ञात करने की विधि

निम्नलिखित चरणों का क्रम फलन के व्युत्क्रम को आसानी से खोजने में मदद करेगा। यहाँ हम एक फलन f(x) = ax + b पर विचार करते हैं, और निम्नलिखित चरणों के माध्यम से इस फलन का व्युत्क्रम खोजने का लक्ष्य रखते हैं।

दिए गए फलन f(x) = ax + b के लिए, f(x) = y को प्रतिस्थापित करें, जिससे y = ax + b प्राप्त होगा।

फलन y = ax + b में x को y से और y को x से प्रतिस्थापित करके x = ay + b प्राप्त करें।

यहाँ y के लिए व्यंजक x = ay + b हल करें। और हमें y = (x - b/a

अंत में y = f-1(x) को प्रतिस्थापित करें, और हमें f-1(x) = (x - b)/a प्राप्त होगा।

फलन का प्रतिलोम

व्युत्क्रम फलन का ग्राफ़

अंतःक्षेपक(इंजेक्टिव) फलन मूल फलन का प्रतिबिंब है जो रेखा $y=x$ के संदर्भ में है, और $(x,y)$ को $(y,x)$ के साथ समागमन(स्वैप) करके प्राप्त किया जाता है।

यदि दो फलन के ग्राफ़ दिए गए हैं, तो हम पहचान सकते हैं कि वे एक दूसरे के व्युत्क्रम हैं या नहीं। यदि दोनों फलन के ग्राफ़ रेखा $y=x$ के संबंध में सममित हैं, तो हम कहते हैं कि दोनों फलन एक दूसरे के व्युत्क्रम हैं। ऐसा इस तथ्य के कारण है कि यदि $(x,y)$ फलन पर स्थित है, तो $(y,x)$ इसके व्युत्क्रम फलन पर स्थित है।

@@ Line 1: / Line 1: @@
-व्युत्क्रम फ़ंक्शन को मूल फ़ंक्शन f के संबंध में f-1 द्वारा दर्शाया जाता है और मूल फ़ंक्शन का डोमेन व्युत्क्रम फ़ंक्शन की श्रेणी बन जाता है और दिए गए फ़ंक्शन की श्रेणी व्युत्क्रम फ़ंक्शन का डोमेन बन जाती है। व्युत्क्रम फ़ंक्शन का ग्राफ़ रेखा y = x के संदर्भ में (x, y) को (y, x) से बदलकर प्राप्त किया जाता है।
+व्युत्क्रम फलन   को मूल फलन   f के संबंध में f-1 द्वारा दर्शाया जाता है और मूल फलन   का डोमेन व्युत्क्रम फलन   की श्रेणी बन जाता है और दिए गए फलन   की श्रेणी व्युत्क्रम फलन   का डोमेन बन जाती है। व्युत्क्रम फलन   का ग्राफ़ रेखा y = x के संदर्भ में (x, y) को (y, x) से बदलकर प्राप्त किया जाता है।
-आइए व्युत्क्रम फ़ंक्शन, व्युत्क्रम फ़ंक्शन को खोजने के चरणों और व्युत्क्रम फ़ंक्शन के ग्राफ़ के बारे में अधिक जानें।
+आइए व्युत्क्रम फ़ंक्शन, व्युत्क्रम फलन   को खोजने के चरणों और व्युत्क्रम फलन   के ग्राफ़ के बारे में अधिक जानें।
-एक फ़ंक्शन मानों को स्वीकार करता है, इन मानों पर विशेष ऑपरेशन करता है और आउटपुट उत्पन्न करता है। व्युत्क्रम फ़ंक्शन परिणामी के साथ सहमत होता है, संचालित होता है और मूल फ़ंक्शन पर वापस पहुँचता है।
+एक फलन   मानों को स्वीकार करता है, इन मानों पर विशेष ऑपरेशन करता है और आउटपुट उत्पन्न करता है। व्युत्क्रम फलन   परिणामी के साथ सहमत होता है, संचालित होता है और मूल फलन   पर वापस पहुँचता है।
 == परिभाषा ==
-फ़ंक्शन f का व्युत्क्रम f-1 द्वारा दर्शाया जाता है और यह केवल तभी मौजूद होता है जब f एक-एक और आच्छादक फ़ंक्शन दोनों हो। ध्यान दें कि f-1, f का व्युत्क्रम नहीं है। फ़ंक्शन f और आच्छादक फ़ंक्शन f-1 की संरचना x का डोमेन मान देती है।
+फलन   f का व्युत्क्रम f-1 द्वारा दर्शाया जाता है और यह केवल तभी मौजूद होता है जब f एक-एक और आच्छादक फलन   दोनों हो। ध्यान दें कि f-1, f का व्युत्क्रम नहीं है। फलन   f और आच्छादक फलन   f-1 की संरचना x का डोमेन मान देती है।
 (f o f-1) (x) = (f-1 o f) (x) = x
-फ़ंक्शन 'f' को व्युत्क्रम फ़ंक्शन माना जाने के लिए, y ∈ Y श्रेणी में प्रत्येक तत्व को डोमेन सेट में किसी तत्व x ∈ X से मैप किया गया है, और इस तरह के संबंध को एक-एक संबंध या निषेधाज्ञा संबंध कहा जाता है। साथ ही दिए गए फ़ंक्शन के व्युत्क्रम f-1 का डोमेन y ∈ Y है जो सह-डोमेन सेट में एक अलग तत्व x ∈ X से संबंधित है, और दिए गए फ़ंक्शन 'f' के संदर्भ में इस तरह का संबंध एक आच्छादक फ़ंक्शन या एक प्रक्षेपण फ़ंक्शन है। इस प्रकार व्युत्क्रम फलन एक निषेधात्मक और एक अधिरोपण फलन होने के कारण, एक द्विआवेशन फलन कहलाता है।
+फलन   'f' को व्युत्क्रम फलन   माना जाने के लिए, y ∈ Y श्रेणी में प्रत्येक तत्व को डोमेन सेट में किसी तत्व x ∈ X से मैप किया गया है, और इस तरह के संबंध को एक-एक संबंध या निषेधाज्ञा संबंध कहा जाता है। साथ ही दिए गए फलन   के व्युत्क्रम f-1 का डोमेन y ∈ Y है जो सह-डोमेन सेट में एक अलग तत्व x ∈ X से संबंधित है, और दिए गए फलन   'f' के संदर्भ में इस तरह का संबंध एक आच्छादक फलन   या एक प्रक्षेपण फलन   है। इस प्रकार व्युत्क्रम फलन एक निषेधात्मक और एक अधिरोपण फलन होने के कारण, एक द्विआवेशन फलन कहलाता है।
-आइए एक फ़ंक्शन f पर विचार करें जिसका डोमेन सेट X है और सहडोमेन सेट Y है। फ़ंक्शन f व्युत्क्रमणीय है यदि कोई अन्य फ़ंक्शन g मौजूद है जिसका डोमेन Y है और इसका सहडोमेन X है। इन दो फ़ंक्शन को f(x) = Y, और g(y) = X के रूप में दर्शाया जा सकता है। इस स्थिति के लिए, यदि फ़ंक्शन f(x) व्युत्क्रम है, तो इसका व्युत्क्रम फ़ंक्शन g(x) अद्वितीय है।
+आइए एक फलन   f पर विचार करें जिसका डोमेन सेट X है और सहडोमेन सेट Y है। फलन   f व्युत्क्रमणीय है यदि कोई अन्य फलन   g मौजूद है जिसका डोमेन Y है और इसका सहडोमेन X है। इन दो फलन   को f(x) = Y, और g(y) = X के रूप में दर्शाया जा सकता है। इस स्थिति के लिए, यदि फलन   f(x) व्युत्क्रम है, तो इसका व्युत्क्रम फलन   g(x) अद्वितीय है।
-यदि दो फ़ंक्शन f(x), और g(x) की संरचना के परिणामस्वरूप एक पहचान फ़ंक्शन f(g(x))= x होता है, तो दोनों फ़ंक्शन एक दूसरे के व्युत्क्रम कहलाते हैं। यदि x पर इनपुट के रूप में फ़ंक्शन के अनुप्रयोग से y का n आउटपुट मिलता है, तो y पर दूसरे फ़ंक्शन g के अनुप्रयोग से x का मान वापस मिलना चाहिए। इसलिए फ़ंक्शन का व्युत्क्रम फ़ंक्शन को उलट देता है। दिए गए फ़ंक्शन का डोमेन व्युत्क्रम फ़ंक्शन की श्रेणी बन जाता है, और दिए गए फ़ंक्शन की श्रेणी व्युत्क्रम फ़ंक्शन का डोमेन बन जाती है।
+यदि दो फलन   f(x), और g(x) की संरचना के परिणामस्वरूप एक पहचान फलन   f(g(x))= x होता है, तो दोनों फलन   एक दूसरे के व्युत्क्रम कहलाते हैं। यदि x पर इनपुट के रूप में फलन   के अनुप्रयोग से y का n आउटपुट मिलता है, तो y पर दूसरे फलन   g के अनुप्रयोग से x का मान वापस मिलना चाहिए। इसलिए फलन   का व्युत्क्रम फलन   को उलट देता है। दिए गए फलन   का डोमेन व्युत्क्रम फलन   की श्रेणी बन जाता है, और दिए गए फलन   की श्रेणी व्युत्क्रम फलन   का डोमेन बन जाती है।
-== व्युत्क्रम फ़ंक्शन खोजने के चरण ==
+== व्युत्क्रम फलन ज्ञात करने की विधि ==
-निम्नलिखित चरणों का क्रम फ़ंक्शन के व्युत्क्रम को आसानी से खोजने में मदद करेगा। यहाँ हम एक फ़ंक्शन f(x) = ax + b पर विचार करते हैं, और निम्नलिखित चरणों के माध्यम से इस फ़ंक्शन का व्युत्क्रम खोजने का लक्ष्य रखते हैं।
+निम्नलिखित चरणों का क्रम फलन   के व्युत्क्रम को आसानी से खोजने में मदद करेगा। यहाँ हम एक फलन   f(x) = ax + b पर विचार करते हैं, और निम्नलिखित चरणों के माध्यम से इस फलन   का व्युत्क्रम खोजने का लक्ष्य रखते हैं।
-दिए गए फ़ंक्शन f(x) = ax + b के लिए, f(x) = y को प्रतिस्थापित करें, जिससे y = ax + b प्राप्त होगा।
+दिए गए फलन   f(x) = ax + b के लिए, f(x) = y को प्रतिस्थापित करें, जिससे y = ax + b प्राप्त होगा।
-फ़ंक्शन y = ax + b में x को y से और y को x से प्रतिस्थापित करके x = ay + b प्राप्त करें।
+फलन   y = ax + b में x को y से और y को x से प्रतिस्थापित करके x = ay + b प्राप्त करें।
 यहाँ y के लिए व्यंजक x = ay + b हल करें। और हमें y = (x - b/a
 अंत में y = f-1(x) को प्रतिस्थापित करें, और हमें f-1(x) = (x - b)/a प्राप्त होगा।
+[[File:फलन का प्रतिलोम.jpg|thumb|फलन का प्रतिलोम]]
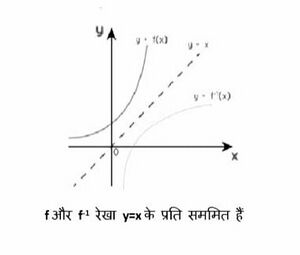
+== व्युत्क्रम फलन का ग्राफ़ ==
+अंतःक्षेपक(इंजेक्टिव) फलन मूल फलन का प्रतिबिंब है जो रेखा <math>y = x</math> के संदर्भ में है, और <math>(x, y)</math> को <math>(y, x)</math>के साथ  समागमन(स्वैप) करके प्राप्त किया जाता है।
+यदि दो फलन के ग्राफ़ दिए गए हैं, तो हम पहचान सकते हैं कि वे एक दूसरे के व्युत्क्रम हैं या नहीं। यदि दोनों फलन  के ग्राफ़ रेखा <math>y = x</math> के संबंध में सममित हैं, तो हम कहते हैं कि दोनों फलन  एक दूसरे के व्युत्क्रम हैं। ऐसा इस तथ्य के कारण है कि यदि <math>(x, y)</math> फलन पर स्थित है, तो <math>(y, x)</math> इसके व्युत्क्रम फलन  पर स्थित है।
-== व्युत्क्रम फ़ंक्शन का ग्राफ़ ==
-इंजेक्टिव फ़ंक्शन मूल फ़ंक्शन का प्रतिबिंब है जो रेखा y = x के संदर्भ में है, और (x, y) को (y, x) के साथ स्वैप करके प्राप्त किया जाता है।
-यदि दो फ़ंक्शन के ग्राफ़ दिए गए हैं, तो हम पहचान सकते हैं कि वे एक दूसरे के व्युत्क्रम हैं या नहीं। यदि दोनों फ़ंक्शन के ग्राफ़ रेखा y = x के संबंध में सममित हैं, तो हम कहते हैं कि दोनों फ़ंक्शन एक दूसरे के व्युत्क्रम हैं। ऐसा इस तथ्य के कारण है कि यदि (x, y) फ़ंक्शन पर स्थित है, तो (y, x) इसके व्युत्क्रम फ़ंक्शन पर स्थित है।
 [[Category:गणित]][[Category:कक्षा-12]]
 [[Category:प्रतिलोम त्रिकोणमितीय फलन]]