वज्र-गुणनखंड विधि

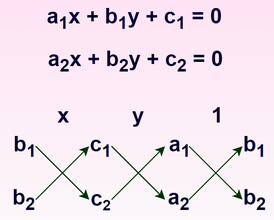
दो चर वाले रैखिक समीकरण युग्म को हल करने की वज्र-गुणनखंड विधि सबसे आसान तरीकों में से एक है ।वज्र-गुणनखंड विधि दो चरों में रैखिक समीकरणों का त्वरित विधि है। इस विधि में , एक भिन्न के अंश को दूसरे के हर से गुणा किया जाता है और पहले पद के हर को दूसरे पद के अंश से गुणा किया जाता है। आइए इस इकाई में हम वज्र-गुणनखंड विधि को विस्तार पूर्वक समझते है ।

वज्र-गुणन विधि की व्युत्पत्ति

दो चर वाले रैखिक समीकरण युग्म को इस प्रकार प्रदर्शित किया जा सकता है ,

$a_{1}x+b_{1}y+c_{1}=0$ $...........(1)$

$a_{2}x+b_{2}y+c_{2}=0$ $...........(2)$

जहां $a_{1},b_{1},c_{1},a_{2},b_{2},c_{2}$ वास्तविक संख्याएं हैं ।

समीकरण $(1)$ को $b_{2}$ से और समीकरण $(2)$ को $b_{1}$ से गुणा करने पर ,

$b_{2}a_{1}x+b_{2}b_{1}y+b_{2}c_{1}=0$ $...........(3)$

$b_{1}a_{2}x+b_{1}b_{2}y+b_{1}c_{2}=0$ $...........(4)$

समीकरण $(4)$ को $(3)$ से घटाने पर ,

$(b_{2}a_{1}-b_{1}a_{2})x+(b_{2}b_{1}-b_{1}b_{2})y+b_{2}c_{1}-b_{1}c_{2}=0$

$(b_{2}a_{1}-b_{1}a_{2})x+b_{2}c_{1}-b_{1}c_{2}=0$

$(b_{2}a_{1}-b_{1}a_{2})x=b_{1}c_{2}-b_{2}c_{1}$

$x={\frac {b_{1}c_{2}-b_{2}c_{1}}{b_{2}a_{1}-b_{1}a_{2}}}$

वज्र-गुणनखंड विधि

$x$ के प्राप्त मान को समीकरण $(1)$ में रखने पर ,

$y={\frac {c_{1}a_{2}-c_{2}a_{1}}{b_{2}a_{1}-b_{1}a_{2}}}$

अतः , समीकरणों का हल इस प्रकार दिया जाएगा ,

${\frac {x}{b_{1}c_{2}-b_{2}c_{1}}}={\frac {y}{c_{1}a_{2}-c_{2}a_{1}}}={\frac {1}{b_{2}a_{1}-b_{1}a_{2}}}$

इसलिए , हम वज्र गुणन विधि का उपयोग करके दो चर में रैखिक समीकरण युग्म का हल आसानी से प्राप्त सकते हैं । उपर्युक्त समीकरण को याद रखने के लिए दिया गया चित्र उपयोगी होगा । दिए गए चित्र में दो संख्याओं के बीच का बाण चिह्न $(\longrightarrow )$ यह दर्शाता हैं कि उन्हें गुणा किया जाएगा और दूसरे गुणनफल को पहले से घटाया जाएगा ।

टिप्पणी

1. यदि ${\frac {a_{1}}{a_{2}}}\neq {\frac {b_{1}}{b_{2}}}$ है , तो हमें एक अद्वितीय हल मिलता है और दो चर में रैखिक समीकरण युग्म संगत है ।
2. यदि ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}={\frac {c_{1}}{c_{2}}}$ , तो अनंत रूप से कई हल हैं और दो चर में रैखिक समीकरण युग्म आश्रित और सुसंगत है ।
3. यदि ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}\neq {\frac {c_{1}}{c_{2}}}$ , तो कोई हल नहीं है और दो चर में रैखिक समीकरण युग्म असंगत है ।

उदाहरण 1

वज्र गुणन विधि का उपयोग करके दो चर वाले निम्नलिखित समीकरण युग्म को हल करें :

$3x-4y=2$

$y-2x=7$

हल

दिए गए समीकरण को दो चरों में रैखिक समीकरण के मानक रूप $a_{1}x+b_{1}y+c_{1}=0$ , $a_{2}x+b_{2}y+c_{2}=0$ में लिखने पर ,

$3x-4y-2=0$ $...........(1)$

$-2x+y-7=0$ $...........(2)$

अतः , समीकरण $(1)$ से , $a_{1}=3$ , $b_{1}=-4$ , $c_{1}=-2$ एवं समीकरण $(2)$ से $a_{2}=-2$ , $b_{2}=1$ , $c_{2}=-7$

उपर्युक्त समीकरण युग्म के हल की प्रकृति ज्ञात करने पर ,

${\frac {a_{1}}{a_{2}}}\neq {\frac {b_{1}}{b_{2}}}$

मान रखने पर ,

${\frac {3}{-2}}\neq {\frac {-4}{1}}$

अतः , यह स्पष्ट है कि उपर्युक्त समीकरण युग्म के हल अद्वितीय होंगे ।

वज्र गुणन विधि प्रयोग करने पर ,

${\frac {x}{b_{1}c_{2}-b_{2}c_{1}}}={\frac {y}{c_{1}a_{2}-c_{2}a_{1}}}={\frac {1}{b_{2}a_{1}-b_{1}a_{2}}}$

मान रखने पर ,

${\frac {x}{(-4)\times (-7)-1\times (-2)}}={\frac {y}{(-2)\times (-2)-(-7)\times 3}}={\frac {1}{1\times 3-(-4)\times (-2)}}$

${\frac {x}{28+2}}={\frac {y}{4+21}}={\frac {1}{3-8}}$

${\frac {x}{30}}={\frac {y}{25}}={\frac {1}{-5}}$

पदो को बराबर करने पर ,

${\frac {x}{30}}={\frac {1}{-5}}$

${\ce {x={\frac {-30}{5}}}}$

$x=-6$

${\frac {y}{25}}={\frac {1}{-5}}$

${\ce {y={\frac {-25}{5}}}}$

${\ce {y=-5}}$

अतः , उपर्युक्त समीकरण युग्म का हल $x=-6,y=-5$ है ।

सत्यापन

समीकरण $(1)$ ,

$3x-4y=2$

मान रखने पर ( $x=-6,y=-5$ ) ,

$3\times (-6)-4\times (-5)=2$

$-18+20=2$

$2=2$

समीकरण $(2)$

$y-2x=7$

मान रखने पर ( $x=-6,y=-5$ ) ,

$-5-2\times (-6)=7$

$-5+12=7$

$7=7$

उदाहरण 2

दो चरों में दिए गए रैखिक समीकरण युग्म के हल की प्रकृति ज्ञात कीजिए :

$2x+3y=7$

$4x+6y=19$

हल

दिए गए समीकरण को दो चरों में रैखिक समीकरण युग्म के मानक रूप $a_{1}x+b_{1}y+c_{1}=0$ , $a_{2}x+b_{2}y+c_{2}=0$ में लिखने पर ,

$2x+3y-7=0$ $...........(1)$

$4x+6y-19=0$ $...........(2)$

अतः , समीकरण $(1)$ से , $a_{1}=2$ , $b_{1}=3$ , $c_{1}=-7$ एवं समीकरण $(2)$ से $a_{2}=4$ , $b_{2}=6$ , $c_{2}=-19$

रैखिक समीकरण युग्म के हल की प्रकृति ज्ञात करने पर ,

${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}\neq {\frac {c_{1}}{c_{2}}}$

मान रखने पर ,

${\frac {2}{4}}={\frac {3}{6}}\neq {\frac {-7}{-19}}$

${\frac {1}{2}}={\frac {1}{2}}\neq {\frac {7}{19}}$

हम जानते हैं , यदि ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}\neq {\frac {c_{1}}{c_{2}}}$ , तो कोई हल नहीं है और दो चर में रैखिक समीकरण युग्म असंगत है ।

उदाहरण 3

दो चरों में दिए गए रैखिक समीकरण युग्म के हल की प्रकृति ज्ञात कीजिए :

$3x-y=3$

$9x-3y=9$

हल

दिए गए समीकरण को दो चरों में रैखिक समीकरण युग्म के मानक रूप $a_{1}x+b_{1}y+c_{1}=0$ , $a_{2}x+b_{2}y+c_{2}=0$ में लिखने पर ,

$3x-y-3=0$ $...........(1)$

$9x-3y-9=0$ $...........(2)$

अतः , समीकरण $(1)$ से , $a_{1}=3$ , $b_{1}=-1$ , $c_{1}=-3$ एवं समीकरण $(2)$ से $a_{2}=9$ , $b_{2}=-3$ , $c_{2}=-9$

रैखिक समीकरण युग्म के हल की प्रकृति ज्ञात करने पर ,

${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}={\frac {c_{1}}{c_{2}}}$

मान रखने पर ,

${\frac {3}{9}}={\frac {-1}{-3}}={\frac {-3}{-9}}$

${\frac {1}{3}}={\frac {1}{3}}={\frac {1}{3}}$

हम जानते हैं , यदि ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}={\frac {c_{1}}{c_{2}}}$ , तो दो चर में रैखिक समीकरण युग्म के अनंत रूप से कई हल हैं और समीकरण युग्म आश्रित और संगत है ।

अभ्यास प्रश्न

वज्र गुणन विधि का उपयोग करके दो चर वाले निम्नलिखित समीकरण युग्म को हल करें :

$7x-15y=2$

$x+2y=3$