अवकलनीयता: Difference between revisions

Latest revision as of 14:21, 30 November 2024

अवकलनीय फलन, कैलकुलस में एक चर में एक फलन होता है, जैसे कि इसका अवकलज इसके पूरे प्रांत में प्रत्येक बिंदु पर उपस्थित होता है। एक अवकलनीय फलन के ग्राफ़ की स्पर्श रेखा सदैव अपने प्रांत में प्रत्येक आंतरिक बिंदु पर गैर-ऊर्ध्वाधर होती है। अवकलनीय फलन में कोई विराम, पुच्छ या कोण नहीं होता है। एक अवकलनीय फलन प्रायः संतत होता है लेकिन हर संतत फलन अवकलनीय नहीं होता है।

इस लेख में, हम अवकलनीय का अर्थ, अवकलनीयता नियमों का उपयोग करके यह पता लगाने के तरीके का पता लगाएंगे कि फलन अवकलनीय है या नहीं, अवकलनीयता में सीमाओं के महत्व को समझेंगे और इसके अन्य प्रभावशाली पहलुओं को ज्ञात करेंगे।

परिभाषा

बिंदु

P={dy \over dx}

पर किसी फलन का अवकलनीयता

किसी फलन को अवकलनीय कहा जाता है यदि फलन का अवकलज उसके प्रांत में सभी बिंदुओं पर उपस्थित हो। विशेष रूप से, यदि फलन $f(x),x=a$ पर अवकलनीय है, तो $f'(a)$ प्रांत में उपस्थित है। आइए हम बहुपद और पारमार्थिक फलन के कुछ उदाहरण देखें जो अवकलनीय हैं:

$f(x)=x^{4}-3x+5$
$f(x)=x^{100}$
$f(x)=sinx$
$f(x)=e^{x}$

अवकलनीय फलनों के नियम

यदि $f,g$ अवकलनीय फलन हैं, तो हम उनके योग, अंतर, गुणनफल और भागफल के अवकलज ज्ञात करने के लिए कुछ नियमों का उपयोग कर सकते हैं। यहाँ कुछ अवकलनीयता सूत्र दिए गए हैं जिनका उपयोग अवकलनीय फलन के अवकलज ज्ञात करने के लिए किया जाता है:

$(f+g)'=f'+g'$
$(f-g)'=f'-g'$
$(fg)'=f'g+fg'$
$\left({\frac {f}{g}}\right)'={\frac {(f'g-fg')}{f^{2}}}$

उदाहरण

आइए फलन का अवकलज ज्ञात करने के लिए अवकलनीयता नियमों का उपयोग करें

$f(x)=(2x+1)^{3}$

${df \over dx}={d(2x+1)^{3} \over dx}$

$={d(8x^{3}+12x^{2}+6x+1) \over dx}$

$=24x^{2}+24x+6$

$=6(2x+1)^{2}$

सामान्य अवकलनीयता सूत्र

कलन में, अवकलनीय फलनों का अवकलन चर के संबंध में फलनों के परिवर्तन की दर निर्धारित करने की गणितीय प्रक्रिया है। कुछ सामान्य अवकलनीयता सूत्र जिनका उपयोग हम विभिन्न गणितीय समस्याओं को हल करने के लिए करते हैं:

$sinx:(sinx)'=cosx$ का अवकलज
$cosx:(cosx)'=-sinx$ का अवकलज
$tanx:(tanx)'=sec^{2}x$ का अवकलज
$cotx:(cotx)'=-cosec^{2}x$ का अवकलज
$secx:(secx)'=secx.tanx$ का अवकलज
$cosecx:(cosecx)'=-cosecx.cotx$ का अवकलज
$x^{n}:(x^{n})'=nx^{n-1}$ का अवकलज
$e^{x}:(e^{x})'=e^{x}$ का अवकलज
$\ln x:(\ln x)'={\frac {1}{x}}$ का अवकलज

अवकलनीय फलनों के लिए सीमा सूत्र

सीमाओं का उपयोग करके यह निर्धारित करने का एक वैकल्पिक तरीका है कि कोई फलन $f(x)$ अवकलनीय है या नहीं। यदि निम्न सीमा उपस्थित है तो फलन $f(x)$ बिंदु $x=a$ पर अवकलनीय है:

$\textstyle \lim _{h\to 0}\displaystyle {\frac {f(c+h)-f(c)}{h}}$

उदाहरण: $f(x)=|x|$ द्वारा दिए गए निरपेक्ष मान फलन पर विचार करें

हम यह निर्धारित करेंगे कि यह फलन $c=0$ पर अवकलनीय है या नहीं। आइए सीमा $\textstyle \lim _{h\to 0}\displaystyle {\frac {f(c+h)-f(c)}{h}}$ ज्ञात करें।

$\textstyle \lim _{h\to 0}\displaystyle {\frac {f(c+h)-f(c)}{h}}=\textstyle \lim _{h\to 0}\displaystyle {\frac {f(0+h)-f(0)}{h}}$

$\textstyle \lim _{h\to 0}\displaystyle {\frac {\left\vert h\right\vert -\left\vert 0\right\vert }{h}}$

$\textstyle \lim _{h\to 0}\displaystyle {\frac {\left\vert h\right\vert }{h}}$

जब $h$ बाईं ओर से $0$ के करीब पहुंचता है तो क्या होता है? आइए फलन के व्यवहार को देखें जब $h$ ऋणात्मक $x$ -अक्ष से $0$ के करीब आता है।

$\textstyle \lim _{h\to 0}\displaystyle {\frac {\left\vert h\right\vert }{h}}=\textstyle \lim _{h\to 0}\displaystyle {\frac {-h}{h}}$

$=-1$

जब $h$ दाईं ओर से $0$ के करीब पहुंचता है तो क्या होता है? अब, आइए फलन के व्यवहार को देखें जब $h$ धनात्मक $x$ -अक्ष से $0$ के करीब आता है।

$\textstyle \lim _{h\to 0}\displaystyle {\frac {\left\vert h\right\vert }{h}}=\textstyle \lim _{h\to 0}\displaystyle {\frac {h}{h}}$

$=1$

क्या आपने देखा कि सीमाएं अलग-अलग हैं?

इसका मतलब यह है कि सीमा $\textstyle \lim _{h\to 0}\displaystyle {\frac {f(c+h)-f(c)}{h}}$ $c=0$ पर $f(x)=|x|$ उपस्थित नहीं है।

इसका तात्पर्य यह है कि निरपेक्ष मान फलन $f(x)=|x|;x=0$ पर अवकलनीय नहीं है।

अवकलनीय फलनों के लिए युक्तियाँ और उपाय

यदि किसी आलेख में किसी बिंदु पर नुकीला कोना(शार्प कार्नर) है, तो फलन उस बिंदु पर अवकलनीय नहीं है।
यदि किसी आलेख में किसी बिंदु पर विराम है, तो फलन उस बिंदु पर अवकलनीय नहीं है।
यदि किसी आलेख में किसी बिंदु पर एक ऊर्ध्वाधर स्पर्श रेखा है, तो फलन उस बिंदु पर अवकलनीय नहीं है।

महत्वपूर्ण टिप्पणियाँ

अवकलनीय फलन वे फलन होते हैं जिनके अवकलज उपस्थित होते हैं।
यदि कोई फलन अवकलनीय है, तो वह सतत होता है।
यदि कोई फलन सतत है, तो वह आवश्यक रूप से अवकलनीय नहीं होता।
अवकलनीय फलन के आलेख में रुकावट, कोने या नोक(कस्प) नहीं होते।

@@ Line 1: / Line 1: @@
-एक अवकलनीय फलन कैलकुलस में एक चर में एक फलन होता है, जैसे कि इसका व्युत्पन्न इसके पूरे प्रांत में प्रत्येक बिंदु पर उपस्थित होता है। एक अवकलनीय फलन के ग्राफ़ की स्पर्श रेखा हमेशा अपने प्रांत में प्रत्येक आंतरिक बिंदु पर गैर-ऊर्ध्वाधर होती है। एक अवकलनीय फलन में कोई विराम, पुच्छ या कोण नहीं होता है। एक अवकलनीय फलन हमेशा निरंतर होता है लेकिन हर निरंतर फलन अवकलनीय नहीं होता है।
+अवकलनीय फलन, कैलकुलस में एक चर में एक फलन होता है, जैसे कि इसका [[अवकलज]]  इसके पूरे प्रांत में प्रत्येक बिंदु पर उपस्थित होता है। एक अवकलनीय फलन के ग्राफ़ की स्पर्श रेखा सदैव अपने प्रांत में प्रत्येक आंतरिक बिंदु पर गैर-ऊर्ध्वाधर होती है। अवकलनीय फलन में कोई विराम, पुच्छ या कोण नहीं होता है। एक अवकलनीय फलन प्रायः संतत होता है लेकिन हर संतत फलन अवकलनीय नहीं होता है।
-इस लेख में, हम अवकलनीय का अर्थ, अवकलनीयता नियमों का उपयोग करके यह पता लगाने के तरीके का पता लगाएंगे कि फलन अवकलनीय है या नहीं, अवकलनीयता में सीमाओं के महत्व को समझेंगे और इसके अन्य दिलचस्प पहलुओं की खोज करेंगे।
+इस लेख में, हम अवकलनीय का अर्थ, अवकलनीयता नियमों का उपयोग करके यह पता लगाने के तरीके का पता लगाएंगे कि फलन अवकलनीय है या नहीं, अवकलनीयता में सीमाओं के महत्व को समझेंगे और इसके अन्य प्रभावशाली पहलुओं को ज्ञात करेंगे।
 == परिभाषा ==
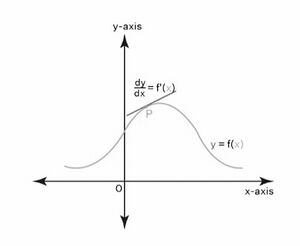
 [[File:अवकलनीयता.jpg|thumb|बिंदु <math>P={dy \over dx}</math> पर किसी फलन का अवकलनीयता]]
-किसी फलन को अवकलनीय कहा जाता है यदि फलन का व्युत्पन्न उसके प्रांत में सभी बिंदुओं पर उपस्थित हो। विशेष रूप से, यदि फलन <math>f(x), x = a</math> पर अवकलनीय है, तो <math>f'(a)</math> प्रांत में उपस्थित है। आइए हम बहुपद और पारमार्थिक फलन के कुछ उदाहरण देखें जो अवकलनीय हैं:
+किसी फलन को अवकलनीय कहा जाता है यदि फलन का अवकलज  उसके प्रांत में सभी बिंदुओं पर उपस्थित हो। विशेष रूप से, यदि [[फलन]] <math>f(x), x = a</math> पर अवकलनीय है, तो <math>f'(a)</math> प्रांत में उपस्थित है। आइए हम [[बहुपद]] और पारमार्थिक फलन के कुछ उदाहरण देखें जो अवकलनीय हैं:
 * <math>f(x) = x^4 - 3x + 5</math>
@@ Line 21: / Line 21: @@
 == उदाहरण ==
-आइए फलन का व्युत्पन्न ज्ञात करने के लिए अवकलनीयता नियमों का उपयोग करें
+आइए फलन का अवकलज  ज्ञात करने के लिए अवकलनीयता नियमों का उपयोग करें
-f(x) = (2x+1)<sup>3</sup>
+<math>f(x) = (2x+1)^3</math>
-df/dx = d(2x+1)<sup>3</sup>/dx
+<math>{df \over dx} = {d(2x+1)^3\over dx}</math>
-= d(8x<sup>3</sup> + 12x<sup>2</sup> + 6x + 1)/dx
+<math>= {d(8x^3 + 12x^2 + 6x + 1) \over dx} </math>
-= 24x<sup>2</sup> + 24x + 6
+<math>= 24x^2 + 24x + 6</math>
-= 6(2x+1)<sup>2</sup>
+<math>= 6(2x+1)^2</math>
 == सामान्य अवकलनीयता सूत्र ==
 कलन में, अवकलनीय फलनों का अवकलन चर के संबंध में फलनों के परिवर्तन की दर निर्धारित करने की गणितीय प्रक्रिया है। कुछ सामान्य अवकलनीयता सूत्र जिनका उपयोग हम विभिन्न गणितीय समस्याओं को हल करने के लिए करते हैं:
-* sin x: (sin x)' = cos x का अवकलज
+* <math>sin x: (sin x)' = cos x</math>  का अवकलज
-* cos x: (cos x)' = -sin x  का अवकलज
+* <math>cos x: (cos x)' = -sin x</math>    का अवकलज
-* tan x: (tan x)' = sec<sup>2</sup> x  का अवकलज
+* <math>tan x: (tan x)' = sec^2 x</math>   का अवकलज
-* cot x: (cot x)' = -cosec<sup>2</sup> x  का अवकलज
+* <math>cot x: (cot x)' = -cosec^2 x</math>  का अवकलज
-* sec x: (sec x)' = sec x.tan x  का अवकलज
+* <math>sec x: (sec x)' = sec x.tan x</math>  का अवकलज
-* cosec x: (cosec x)' = -cosec x.cot x  का अवकलज
+* <math>cosec x: (cosec x)' = -cosec x.cot x</math>  का अवकलज
-* x<sup>n</sup>: (x<sup>n</sup>)' = nx<sup>n-1</sup>  का अवकलज
+* <math>x^n: (x^n)' = nx^{n-1}</math>  का अवकलज
-* e<sup>x</sup>: (e<sup>x</sup>)' = e<sup>x</sup>  का अवकलज
+* <math>e^x: (e^x)' = e^x</math>  का अवकलज
-* ln x: (ln x)' = 1/x का अवकलज
+* <math>\ln x: (\ln x)' = \frac{1}{x}</math>   का अवकलज
 == अवकलनीय फलनों के लिए सीमा सूत्र ==
-सीमाओं का उपयोग करके यह निर्धारित करने का एक वैकल्पिक तरीका है कि कोई फलन <math>f(x)</math> अवकलनीय है या नहीं। यदि निम्न सीमा उपस्थित है तो फलन <math>f(x)</math> बिंदु<math>x = a</math> पर अवकलनीय है:
+सीमाओं का उपयोग करके यह निर्धारित करने का एक वैकल्पिक तरीका है कि कोई फलन <math>f(x)</math> अवकलनीय है या नहीं। यदि निम्न सीमा उपस्थित है तो फलन <math>f(x)</math> बिंदु <math>x = a</math> पर अवकलनीय है:
-limh→0f(c+h)−f(c)h
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ f(c+h)-f(c)}{h}</math>
 उदाहरण: <math>f(x) = |x|</math> द्वारा दिए गए निरपेक्ष मान फलन पर विचार करें
-हम यह निर्धारित करेंगे कि यह फलन <math>c = 0</math> पर अवकलनीय है या नहीं। आइए सीमा ज्ञात करें
+हम यह निर्धारित करेंगे कि यह फलन <math>c = 0</math> पर अवकलनीय है या नहीं। आइए सीमा  <math>\textstyle \lim_{h \to 0} \displaystyle \frac{ f(c+h)-f(c)}{h}</math>   ज्ञात करें।
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ f(c+h)-f(c)}{h}= \textstyle \lim_{h \to 0} \displaystyle \frac{ f(0+h)-f(0)}{h}</math>
-जब <math>h</math> बाईं ओर से <math>0</math> के करीब पहुंचता है तो क्या होता है? आइए फलन के व्यवहार को देखें जब <math>h</math> ऋणात्मक <math>x</math>-अक्ष से <math>0</math> के करीब आता है।
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ \left\vert h \right\vert-\left\vert 0 \right\vert}{h}</math>
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ \left\vert h \right\vert}{h}</math>
+जब <math>h</math> बाईं ओर से <math>0</math> के करीब पहुंचता है तो क्या होता है? आइए फलन के व्यवहार को देखें जब <math>h</math> ऋणात्मक <math>x</math>-अक्ष से <math>0</math> के करीब आता है।
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ \left\vert h \right\vert}{h}= \textstyle \lim_{h \to 0} \displaystyle \frac{ - h }{h}</math>
+<math>=-1</math>
 जब <math>h</math> दाईं ओर से <math>0</math> के करीब पहुंचता है तो क्या होता है? अब, आइए फलन के व्यवहार को देखें जब <math>h</math> धनात्मक <math>x</math>-अक्ष से <math>0</math> के करीब आता है।
+<math>\textstyle \lim_{h \to 0} \displaystyle \frac{ \left\vert h \right\vert}{h}= \textstyle \lim_{h \to 0} \displaystyle \frac{ h }{h}</math>
+<math>=1</math>
 क्या आपने देखा कि सीमाएं अलग-अलग हैं?
-इसका मतलब यह है कि सीमा
-पर उपस्थित नहीं है
+इसका मतलब यह है कि सीमा <math>\textstyle \lim_{h \to 0} \displaystyle \frac{ f(c+h)-f(c)}{h}</math>  <math>c = 0</math>  पर <math>f(x) = |x|</math> उपस्थित नहीं है।
-इसका तात्पर्य यह है कि निरपेक्ष मान फलन <math>f(x) = |x| x = 0</math> पर अवकलनीय नहीं है।
+इसका तात्पर्य यह है कि निरपेक्ष मान फलन <math>f(x) = |x| ; x = 0</math> पर अवकलनीय नहीं है।
 == अवकलनीय फलनों के लिए युक्तियाँ और उपाय ==
@@ Line 80: / Line 93: @@
 == महत्वपूर्ण टिप्पणियाँ ==
-* अवकलनीय फलन वे फलन होते हैं जिनके व्युत्पन्न उपस्थित होते हैं।
+* अवकलनीय फलन वे फलन होते हैं जिनके अवकलज  उपस्थित होते हैं।
 * यदि कोई फलन अवकलनीय है, तो वह सतत होता है।
 * यदि कोई फलन सतत है, तो वह आवश्यक रूप से अवकलनीय नहीं होता।